|
Século XIX
Hermann
Ebbinghaus (1850-1909) foi o primeiro psicólogo a aplicar métodos experimentais no estudo da memória. No livro Über das
Gedächtnis, publicado em 1885, encontra-se descrito seu trabalho. A primeira tradução para o inglês, publicada em 1913,
intitulou-se Memory: A Contribution to Experimental Psychology; tal obra colocaremos a disposição seguidamente.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
Author's Preface
In the realm of mental phenomena, experiment and measurement have hitherto been chiefly limited in application to sense
perception and to the time relations of mental processes. By means of the following investigations we have tried to go a step
farther into the workings of the mind and to submit to an experimental and quantitative treatment the manifestations of memory.
The term, memory, is to be taken here in its broadest sense, including Learning, Retention, Association and Reproduction.
The principal objections which, as a matter of course, rise against the possibility of such a treatment are discussed in
detail in the text and in part have been made objects of investi-gation. I may therefore ask those who are not already convinced
a priori of the impossibility of such an attempt to postpone their decision about its practicability.
The author will be pardoned the publication of preliminary results in view of the difficulty of the subject investigated
and the time-consuming character of the tests. Justice demands that the many defects due to incompleteness shall not be raised
as objections against such results. The tests were all made upon myself and have primarily only individual significance. Naturally
they will not reflect exclusively mere idiosyncrasies of my mental organisation; if the absolute values found are throughout
only individual, yet many a relation of general validity will be found in the relation of these numbers to each other or in
the relations of the relations. But where this is the case and where it is not, I can hope to decide only after finishing
the further and comparative experiments with which I am occupied.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)Translated by Henry A. Ruger & Clara E. Bussenius (1913)
Originally published in New
York by Teachers College, Columbia University.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER I
OUR KNOWLEDGE CONCERNING MEMORY
Section 1. Memory in its Effects
The language of life as well as of science in attributing a memory to the mind attempts to point out the facts and their
interpretation somewhat as follows:
Mental states of every kind, -- sensations, feelings, ideas, -- which were at one time present in consciousness and then
have disappeared from it, have not with their disappearance absolutely ceased to exist. Although the inwardly-turned look
may no longer be able to find them, nevertheless they have not been utterly destroyed and annulled, but in a certain manner
they continue to exist, stored up, so to speak, in the memory. We cannot, of course, directly observe their present existence,
but it is revealed by the effects which come to our knowledge with a certainty like that with which we infer the existence
of the stars below the horizon. These effects are of different kinds.
In a first group of cases we can call back into consciousness by an exertion of the will directed to this purpose the seemingly
lost states (or, indeed, in case these consisted in immediate sense-perceptions, we can recall their true memory images) that
is, we can reproduce them voluntarily. During attempts of this sort, -- that is, attempts to recollect -- all sorts
of images toward which our aim was not directed, accompany the desired images to the light of consciousness. Often, indeed,
the latter entirely miss the goal, but as a general thing among the representations is found the one which we sought, and
it is immediately recognised as something formerly experienced. It wou1d be absurd to suppose that our will has created it
anew and, as it were, out of nothing; it must have been present somehow or somewhere. The will,
so to speak, has only discovered it and brought it to us again.
In a second group of cases this survival is even more striking. Often, even after years, mental states once present in
consciousness return to it with apparent spontaneity and without any act of the will; that is, they are reproduced involuntarily.
Here, also, in the majority of cases we at once recognise the returned mental state as one that has already been experienced;
that is, we remember it. Under certain conditions, however, this accompanying consciousness is lacking, and we know only indirectly
that the "now" must be identical with the "then"; yet we receive in this way a no less valid proof for its existence during
the intervening time. As more exact observation teaches us, the occurrence of these involuntary reproductions is not an entirely
random and accidental one. On the contrary they are brought about through the instrumentality of other immediately present
mental images. Moreover they occur in certain regular ways which in general terms are described under the so-called 'laws
of association.'
Finally there is a third and large group to be reckoned with here. The vanished mental states give indubitable proof of
their continuing existence even if they themselves do not return to consciousness at all, or at least not exactly at the given
time. Employment of a certain range of thought facilitates under certain conditions the employment of a similar range of thought,
even if the former does not come before the mind directly either in its methods or in its results. The boundless domain of
the effect of accumulated experience belongs here. This effect results from the frequent conscious occurrence of any condition
or process, and consists in facilitating the occurrence and progress of similar processes. This effect is not fettered by
the condition that the factors constituting the experience shall return in toto to consciousness. This may incidentally
be the case with a part of them; it must not happen to a too great extent and with too great clearness, otherwise the course
of the present process will immediately be disturbed. Most of these experiences remain concealed from consciousness and yet
produce an effect which is significant and which authenticates their previous existence.
Section 2. Memory in its Dependence
Along with this bare knowledge of the existence of memory and its effects, there is abundant knowledge concerning
the conditions upon which depend the vitality of that inner survival as well as the fidelity and promptness of the
reproduction.
How differently do different individuals behave in this respect! One retains and reproduces well; another, poorly.
And not only does this comparison hold good when different individuals are compared with each other, but also when different
phases of the existence of the same individual are compared: morning and evening, youth and old age, find him different in
this respect.
Differences in the content of the thing to be reproduced are of great influence. Melodies may become a source of
torment by the undesired persistency of their return. Forms and colors are not so importunate; and if they do return, it is
with noticeable loss of clearness and certainty. The musician writes for the orchestra what his inner voice sings to him;
the painter rarely relies without disadvantage solely upon the images which his inner eye presents to him; nature gives him
his forms, study governs his combinations of them. It is with something of a struggle that past states of feeling are realized;
when realized, and this is often only through the instrumentality of the movements which accompanied them, they are but pale
shadows of themselves. Emotionally true singing is rarer than technically correct singing.
If the two foregoing points of view are taken together -- differences in individuals and differences in content -- an endless
number of differences come to light. One individual overflows with poetical reminiscences, another directs symphonies from
memory, while numbers and formulae, which come to a third without effort, slip away from the other two as from a polished
stone.
Very great is the dependence of retention and reproduction upon the intensity of the attention and interest which
were attached to the mental states the first time they were present. The burnt child shuns the fire, and the dog which has
been beaten runs from the whip, after a single vivid experience. People in whom we are interested we may see daily and yet
not be able to recall the color of their hair or of their eyes.
Under ordinary circumstances, indeed, frequent repetitions are indispensable in order to make possible the reproduction
of a given content. Vocabularies, discourses, and poems of any length cannot be learned by a single repetition even with the
greatest concentration of attention on the part of an individual of very great ability. By a sufficient number of repetitions
their final mastery is ensured, and by additional later reproductions gain in assurance and ease is secured.
Left to itself every mental content gradually loses its capacity for being revived, or at least suffers loss in this regard
under the influence of time. Facts crammed at examination time soon vanish, if they were not sufficiently grounded by other
study and later subjected to a sufficient review. But even a thing so early and deeply founded as one's mother tongue is noticeably
impaired if not used for several years.
Section 3. Deficiencies in our Knowledge concerning Memory
The foregoing sketch of our knowledge concerning memory makes no claim to completeness. To it might be added such a series
of propositions known to psychology as the following: "He who learns quickly also forgets quickly," "Relatively long series
of ideas are retained better than relatively short ones," Old people forget most quickly the things they learned last," and
the like. Psychology is wont to make the picture rich with anecdote and illustration. But -- and this is the main point --
even if we particularise our knowledge by a most extended use of illustrative material, everything that we can say retains
the indefinite, general, and comparative character of the propositions quoted above. Our information comes almost exclusively
from the observation of extreme and especially striking cases. We are able to describe these quite correctly in a general
way and in vague expressions of more or less. We suppose, again quite correctly, that the same influences exert themselves,
although in a less degree, in the case of the inconspicuous, but a thousand-fold more frequent, daily activities of memory.
But if our curiosity carries us further and we crave more specific and dependencies, both those already mentioned and others,
-- if we put questions, so to speak, concerning their inner structure -- our answer is silence. How does the disappearance
of the ability to reproduce, forgetfulness, depend upon the length of time during which no repetitions have taken place? What
proportion does the increase in certainty of reproduction bear to the number of repetitions? How do these relations vary with
the greater or less intensity of the interest in the thing to be reproduced? These and similar questions no one can answer.
This inability does not arise from a chance neglect of investigation of these relations. We cannot say that tomorrow, or
whenever we wish to take time, we can investigate these problems. On the contrary this inability is inherent in the nature
of the questions themselves. Although the conceptions in question -- namely, degrees of forgetfulness, of certainty and interest
-- are quite correct, we have no means for establishing such degrees in our experience except at the extremes, and even then
we cannot accurately limit those extremes. We feel therefore that we are not at all in a condition to undertake the investigation.
We form certain conceptions during striking experiences, but we cannot find any realisation of them in the similar but less
striking experiences of everyday life. Vice versa there are probably many conceptions which we have not as yet formed
which would be serviceable and indispensable for a clear understanding of the facts, and their theoretical mastery.
The amount of detailed information which an individual has at his command and his theoretical elaborations of the same
are mutually dependent; they grow in and through each other. It is because of the indefinite and little specialised character
of our knowledge that the theories concerning the processes of memory, reproduction, and association have been up to the present
time of so little value for a proper comprehension of those processes. For example, to express our ideas concerning their
physical basis we use different metaphors-stored up ideas, engraved images, well-beaten paths. There is only one thing certain
about these figures of speech and that is that they are not suitable.
Of course the existence of all these deficiencies has its perfectly sufficient basis in the extraordinary difficulty and
complexity of the matter. It remains to be proved whether, in spite of the clearest insight into the inadequacy of our knowledge,
we shall ever make any actual progress. Perhaps we shall always have to be resigned to this. But a somewhat greater accessibility
than has so far been realised in this field cannot be denied to it, as I hope to prove presently. If by any chance a way to
a deeper penetration into this matter should present itself, surely, considering the significance of memory for all mental
phenomena, it should be our wish to enter that path at once. For at the very worst we should prefer to see resignation arise
from the failure of earnest investigations rather than from persistent, helpless astonishment in the face of their difficulties.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER II
THE POSSIBILITY OF ENLARGING OUR KNOWLEDGE OF MEMORY
Section 4. The Method of Natural Science
The method of obtaining exact measurements -- i.e., numerically exact ones -- of the inner structure of causal relations
is, by virtue of its nature, of general validity. This method, indeed, has been so exclusively used and so fully worked out
by the natural sciences that, as a rule, it is defined as something peculiar to them, as the method of natural science.
To repeat, however, its 1ogical nature makes it generally applicable to all spheres of existence and phenomena. Moreover,
the possibility of defining accurately and exactly the actual behavior of any process whatever, and thereby of giving a reliable
basis for the direct comprehension of its connections depends above all upon the possibility of applying this method.
We all know of what this method consists: an attempt is made to keep constant the mass of conditions which have proven
themselves causally connected with a certain result; one of these conditions is isolated from the rest and varied in a way
that can be numerically described; then the accompanying change on the side of the effect is ascertained by measurement or
computation.
Two fundamental and insurmountable difficulties, seem, however, to oppose a transfer of this method to the investigation
of the causal relations of mental events in general and of those of memory in particular. In the first place, how are we to
keep even approximately constant the bewildering mass of causal conditions which, in so far as they are of mental nature,
almost completely elude our control, and which, moreover, are subject to endless and incessant change? In the second place,
by what possible means are we to measure numerically the mental processes which filt by so quickly and which on introspection
are so hard to analyse? I shall first discuss the second difficulty in connection, of course, with memory, since that is our
present concern.
Section 5. Introduction of Numerical Measurements for Memory Contents
If we consider once more the conditions of retention and reproduction mentioned above (sec. 2), but now with regard to
the possibility of computation, we shall see that with two of them, at least, a numerical determination and a numerical variation
are possible. The different times which elapse between the first production and the reproduction of a series of ideas can
be measured and the repetitions necessary to make these series reproducible can be counted. At first sight, however, there
seems to be nothing similar to this on the side of the effects. Here there is only one alternative, a reproduction is either
possible or it is not possible. It takes place or it does not take place. Of course we take for granted that it may approach,
under different conditions, more or less near to actual occurrence so that in its subliminal existence the series possesses
graded differences. But as long as we limit our observations to that which, either by chance or at the call of our will, comes
out from this inner realm, all these differences are for us equally non-existent.
By somewhat less dependence upon introspection we can, however, by indirect means force these difference into the open.
A poem is learned by heart and then not again repeated. We will suppose that after a half year it has been forgotten: no effort
of recollection is able to call it back again into consciousness. At best only isolated fragments return. Suppose that the
poem is again learned by heart. It then becomes evident that, although to all appearances totally forgotten, it still in a
certain sense exists and in a way to be effective. The second learning requires noticeably less time or a noticeably smaller
number of repetitions than the first. It also requires less time or repetitions than would now be necessary to learn a similar
poem of the same length. In this difference in time and number of repetitions we have evidently obtained a certain measure
for that inner energy which a half year after the first learning still dwells in that orderly complex of ideas which make
up the poem. After a shorter time we should expect to find the difference greater; after a longer time we should expect to
find it less. If the first committing to memory is a very careful and long continued one, the difference will be greater than
if it is desultory and soon abandoned.
In short, we have without doubt in these differences numerical expressions for the difference between these subliminally
persistent series of ideas, differences which otherwise we would have to take for granted and would not be able to demonstrate
by direct observation. Therewith we have gained possession of something that is at least like that which we are seeking in
our attempt to get a foothold for the application of the method of the natural sciences: namely, phenomena on the side of
the effects which are clearly ascertainable, which vary in accordance with the variation of conditions, and which are capable
of numerical determination. Whether we possess in them correct measures for these inner differences, and whether we can achieve
through them correct conceptions as to the causal relations into which this hidden mental life enters -- these questions cannot
be answered a priori. Chemistry is just as little able to determine a priori whether it is the
electrical phenomena, or the thermal, or some other accompaniment of the process of chemical union, which gives it its correct
measure of the effective forces of chemical affinity. There is only one way to do this, and that is to see whether it is possible
to obtain, on the presupposition of the correctness of such an hypothesis, well classified, uncontradictory results, and correct
anticipations of the future.
Instead of the simple phenomenon -- occurrence or non-occurrence of a reproduction -- which admits of no numerical distinction,
I intend therefore to consider from the experimental standpoint a more complicated process as the effect, and I shall observe
and measure its changes as the conditions are varied. By this I mean the artificial bringing about by an appropriate number
of repetitions of a reproduction which would not occur of its own accord.
But in order to realise this experimentally, two conditions at least must be fulfilled.
In the first place, it must be possible to define with some certainty the moment when the goal is reached -- i.e.,
when the process of learning by heart is completed. For if the process of learning by heart is sometimes carried past that
moment and sometimes broken off before it, then part of the differences found under the varying circumstances would be due
to this inequality, and it would be incorrect to attribute it solely to inner differences in the series of ideas. Consequently
among the different reproductions of, say, a poem, occurring during the process of its memorisation, the experimenter must
single out one as especially characteristic, and be able to find it again with practical accuracy.
In the second place the presupposition must be allowed that the number of repetitions by means of which, the other conditions
being unchanged, this characteristic reproduction is brought about would be every time the same. For if this number, under
conditions otherwise equivalent, is now this and now that, the differences arising from varied conditions lose, of course,
all significance for the critical evaluation of those varying conditions.
Now, as far as the first condition is concerned, it is easily fulfilled wherever you have what may properly be called learning
by heart, as in the case of poems, series of words, tone-sequences, and the like. Here, in general, as the number of repetitions
increases, reproduction is at first fragmentary and halting; then it gains in certainty; and finally takes place smoothly
and without error. The first reproduction in which this last result appears can not only be singled out as especially characteristic,
but can also be practically recognised. For convenience I will designate this briefly as the first possible reproduction.
The question now is: -- Does this fulfill the second condition mentioned above? Is the number of repetitions necessary
to bring about this reproduction always the same, the other conditions being equivalent?
However, in this form, the question will be justly rejected because it forces upon us, as if it were an evident supposition,
the real point in question, the very heart of the matter, and admits of none but a misleading answer. Anyone will be ready
to admit without hesitation that this relation of dependence will be the same if perfect equality of experimental condition
is maintained. The much invoked freedom of the will, at least, has hardly ever been misunderstood by anybody so far as to
come in here. But this theoretical constancy is of little value: How shall I find it when the circumstances under which I
am actually forced to make my observations are never the same? So I must rather ask :-- Can I bring under my control the inevitably
and ever fluctuating circumstances and equalise them to such an extent that the constancy presumably existent in the causal
relations in question becomes visible and palpable to me?
Thus the discussion of the one difficulty which opposes an exact examination of the causal relations in the mental sphere
has led us of itself to the other (sec. 4). A numerical determination of the interdependent changes of cause and effect appears
indeed possible if only we can realise the necessary uniformity of the significant conditions in the repetition of our experiments.
Section 6. The Possibility of Maintaining the Constancy of Conditions Requisite for Research
He who considers the complicated processes of the higher mental life or who is occupied with the still more complicated
phenomena of the state and of society will in general be inclined to deny the possibility of keeping constant the conditions
for psychological experimentation. Nothing is more familiar to us than the capriciousness of mental life which brings to nought
all foresight and calculation. Factors which are to the highest degree determinative and to the same extent changeable, such
as mental vigor, interest in the subject, concentration of attention, changes in the course of thought which have been brought
about by sudden fancies and resolves -- all these are either not at all under our control or are so only to an unsatisfactory
extent.
However, care must be taken not to ascribe too much weight to these views, correct in themselves, when dealing with fields
other than those of the processes by the observation of which these views were obtained. All such unruly factors are of the
greatest importance for higher mental processes which occur only by an especially favorable concurrence of circumstances.
The more lowly, commonplace, and constantly occurring processes are not in the least withdrawn from their influence, but we
have it for the most part in our power, when it is a matter of consequence, to make this influence only slightly disturbing.
Sensorial perception, for example, certainly occurs with greater or less accuracy according to the degree of interest; it
is constantly given other directions by the change of external stimuli and by ideas. But, in spite of that, we are on the
whole sufficiently able to see a house just when we want to see it and to receive practically the same picture of it ten times
in succession in case no objective change has occurred.
There is nothing a priori absurd in the assumption that ordinary retention and reproduction, which, according
to general agreement, is ranked next to sensorial perception, should also behave like it in this respect. Whether this is
actually the case or not, however, I say now as I said before, cannot be decided in advance. Our present knowledge is much
too fragmentary, too general, too largely obtained from the extraordinary to enable us to reach a decision on this point by
its aid; that must be reserved for experiments especially adapted to that purpose. We must try in experimental fashion to
keep as constant as possible those circumstances whose influence on retention and reproduction is known or suspected,
and then ascertain whether that is sufficient. The material must be so chosen that decided differences of interest are, at
least to all appearances, excluded; equality of attention may be promoted by preventing external disturbances; sudden fancies
are not subject to control, but, on the whole, their disturbing effect is limited to the moment, and will be of comparatively
little account if the time of the experiment is extended, etc.
When, however, we have actually obtained in such manner the greatest possible constancy of conditions attainable by us,
how are we to know whether this is sufficient for our purpose? When are the circumstances, which will certainly offer differences
enough to keen observation, sufficient1y constant? The answer may be made: -- When upon repetition of the experiment the results
remain constant. The latter statement seems simple enough to be self-evident, but on closer approach to the matter still another
difficulty is encountered.
Section 7. Constant Averages
When shall the results obtained from repeated experiments under circumstances as much alike as possible pass for constant
or sufficiently constant? Is it when one result has the same value as the other or at least deviates so little from it that
the difference in proportion to its own quantity and for our purposes is of no account?
Evidently not. That would be asking too much, and is not necessarily obtained even by the natural sciences. Then, perhaps
it is when the averages from larger groups of experiments exhibit the characteristics mentioned above?
Again evidently not. That would be asking too little. For, if observation of processes that resemble each other from any
point of view are thrown together in sufficiently large numbers, fairly constant mean values are almost everywhere obtained
which, nevertheless, possess little or no importance for the purposes which we have here. The exact distance of two signal
poles, the position of a star at a certain hour, the expansion of a metal for a certain increase of temperature, all the numerous
coefficients and other constants of physics and chemistry are given us as average values which only approximate to a high
degree of constancy. On the other hand the number of suicides in a certain month, the average length of life in a given place,
the number of teams and pedestrians per day at a certain street corner, and the like, are also noticeably constant, each being
an average from large groups of observations. But both kinds of numbers, which I shall temporarily denote as constants
of natural science and statistical constants, are, as everybody knows, constant from different causes and with
entirely different significance for the knowledge of causal relations.
These differences can be formulated as follows: --
In the case of the constants of the natural sciences each individual effect is produced by a combination of causes exactly
alike. The individual values come out somewhat differently because a certain number of those causes do not always join the
combination with exactly the same values (e.g., there are little errors in the adjustment and reading of the
instruments, irregularities in the texture or composition of the material examined or employed, etc.). However, experience
teaches us that this fluctuation of separate causes does not occur absolutely irregularly but that as a rule it runs through
or, rather, tries out limited and comparatively small circles of values symmetrically distributed around a central value.
If several cases are brought together the effects of the separate deviations must more
and more compensate each other and thereby be swallowed up in the central value around which they occur. And the final
result of combining the values will be approximately the same as if the actually changeable causes had remained the same not
only conceptually but also numerically. Thus, the average value is in these cases the adequate numerical representative of
a conceptually definite and well limited system of causal connections; if one part of the system is varied, the accompanying
changes of the average value again give the correct measure for the effect of those deviations on the total complex.
On the other hand, no matter from what point of view statistical constants may be considered it cannot be said of them
that each separate value has resulted from the combination of causes which by themselves had fluctuated within tolerably narrow
limits and in symmetrical fashion. The separate effects arise, rather, from an oftimes inextricable multiplicity of causal
combinations of very different sorts, which, to be sure, may share numerous factors with each other, but which, taken as a
whole, have no conceivable community and actually correspond only in some one characteristic of the effects. That the value
of the separate factors must be very different is, so to say, self evident. That, nevertheless, approximately constant values
appear even here by the combining of large groups -- this fact we may make intelligible by saying that in equal and tolerably
large intervals of time or extents of space the separate causal combinations will be realised with approximately equal frequency;
we do this without doing more than to acknowledge as extant a peculiar and marvellous arrangement of nature. Accordingly these
constant mean values represent no definite and separate causal systems but combinations of such which are by no means of themselves
transparent. Therefore their changes upon variation of conditions afford no genuine measure of the effects of these variations
but only indications of them. They are of no direct value for the setting up of numerically exact relations of dependence
but they are preparatory to this.
Let us now turn back to the question raised at the beginning of this section. When may we consider that this equality of
conditions which we have striven to realise experimentally has been attained? The answer runs as follows: When the average
values of several observations are approximately constant and when at the same time we may assume that the separate cases
belong to the same causal system, whose elements, however, are not limited to exclusively constant values, but may run through
small circles of numerical values symmetrical around a middle value.
Section 8. The Law of Errors
Our question, however, is not answered conclusively by the statement just made. Suppose we had in some way found satisfactorily
constant mean values for some psychical process, how would we go about it to learn whether we might or might not assume a
homogeneous causal condition, necessary for their further utilisation? The physical scientist generally knows beforehand that
he will have to deal with a single causal combination, the statistician knows that he has to deal with a mass of them, ever
inextricable despite all analysis. Both know this from the elementary knowledge they already possess of the nature of the
processes before they proceed with the more detailed investigations. Just as, a moment ago, the present knowledge of psychology
appeared to us too vague and unreliable to be depended upon for decision about the possibility of constant experimental conditions;
so now it may prove insufficient to determine satisfactorily whether in a given case we have to deal with a homogeneous causal
combination or a manifold of them which chance to operate together. The question is, therefore, whether we may throw light
on the nature of the causation of the results we obtain under conditions as uniform as possible by the help of some other
criterion.
The answer must be: This cannot be done with absolute certainty, but can, nevertheless, be done with great probability.
Thus, a start has been made from presuppositions as similar as possible to those by which physical constants have been obtained
and the consequences which flow from them have been investigated. This has been done for the distribution of the single values
about the resulting central value and quite independently of the actual concrete characteristics of the causes. Repeated comparisons
of these calculated values with actual observations have shown that the similarity of the suppositions is indeed great enough
to 1ead to an agreement of the result. The outcome of these speculations closely approximates to reality. It consists in this,
-- that the grouping of a large number of separate values that have arisen from causes of the same kind and with the modifications
repeatedly mentioned, may be correctly represented by a mathematical formula, the so-called Law of Errors. This is especially
characterised by the fact that it contains but one unknown quantity. This unknown quantity measures the relative compactness
of the distribution of the separate values around their central tendency. It therefore changes according to the kind of observation
and is determined by calculation from the separate values.
NOTE. For further information concerning this formula, which is not here our concern, I must refer to the text-books on
the calculation of probabilities and on the theory of errors. For readers unfamiliar with the latter a graphic explanation
will be more comprehensible than a statement and discussion of the formula. Imagine a certain observation to be repeated 1,000
times. Each observation as such is represented by a space of one square millimeter, and its numerical value, or rather its
deviation from the central value of the whole 1,000 observations, by its position on the horizontal line p q of the
adjoining Figure 1. 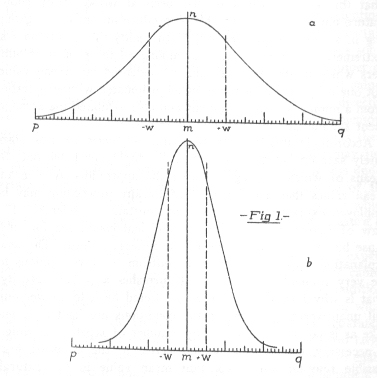
For every observation which exactly corresponds with the central value one square millimeter is laid off on the vertical
line m n. For each observed value which deviates by one unit from the central value upward one square millimeter is
laid off on a vertical line to right of m n and distant one millimeter from it, etc. For every observed value which
deviates by x units above (or below) the central value, one sq. mm. is placed on a vertical line distant from m
n by x mms., to the right (or left, for values below the central value). When all the observations are arranged
in this way the outer contour of the figure may be so compacted that the projecting corners of the separate squares are transformed
into a symmetrical curve. If now the separate measures are of such a sort that their central value may be considered as a
constant as conceived by physical science, the form of the resulting curve is of the kind marked a and b in
Fig. 1. If the middle value is a statistical constant, the curve may have any sort of a form. (The curves a and b
with the lines p q include in each case an area of 1,000 sq. mms. This is strictly the case only with indefinite
prolongation of the curves and the lines p q, but these lines and curves finally approach each other so closely that
where the drawing breaks off only two or three sq. mms. at each end of the curve are missing from the full number. Whether,
for a certain group of observations, the curve has a more steep or more flat form depends on the nature of those observations.
The more exact they are, the more will they pile up around the central value; and the more infrequent the large deviations,
the steeper will the curve be and vice versa. For the rest the law of formation of the curve is always the same. Therefore,
if a person, in the case of any specific combination of observations, obtains any measure of the compactness of distribution
of the observations, he can survey the grouping of the whole mass. He could state, for instance, how often a deviation of
a certain value occurs and how many deviations fall between certain limits. Or -- as I shall show in what follows -- he may
state what amount of variation includes between itself and the central value a certain per cent of all the observed values.
The lines +w and -w of our figure, for instance, cut out exactly the central half of the total space representing
the observations. But in the case of the more exact observations of 1b they are only one half as far from m n as
in 1a. So the statement of their relative distances gives also a measure of the accuracy of the observations.
Therefore, it may be said: wherever a group of effects may be considered as having originated each time from the same causal
combination, which was subject each time only to so-called accidental disturbances, then these values arrange themselves in
accordance with the "law of errors."
However, the reverse of this proposition is not necessarily true, namely, that wherever a distribution of values occurs
according to the law of errors the inference may be drawn that this kind of causation has been at work. Why should nature
not occasionally be able to produce an analogous grouping in a more complicated way? In reality this seems only an extremely
rare occurrence. For among all the groups of numbers which in statistics are usually condensed into mean values not one has
as yet been found which originated without question from a number of causal systems and also exhibited the arrangement summarised
by the "law of errors."[1]
Accordingly, this law may be used as a criterion, not an absolutely safe one to be sure, but still a highly probable one,
by means of which to judge whether the approximately constant mean values that may be obtained by any proceeding may be employed
experimentally as genuine constants of science. The Law of Errors does not furnish sufficient conditions for such a use but
it does furnish one of the necessary ones. The final explanation must depend upon the outcome of investigations to the very
foundations of which it furnishes a certain security. That is why I applied the measure offered by it to answer our still
unanswered question: If the conditions are kept as much alike as is possible, is the average number of repetitions, which
is necessary for learning similar series to the point of first possible reproduction, a constant mean value in the natural
science sense? And I may anticipate by saying that in the case investigated the answer has come out in the affirmative.
Section 9. Resumé
Two fundamental difficulties arise in the way of the application of the so-called Natural Science Method to the examination
of psychical processes:
(1) The constant flux and caprice of mental events do not admit of the establishment of stable experimental conditions.
(2) Psychical processes offer no means for measurement or enumeration.
In the case of the special field of memory (learning, retention, reproduction) the second difficulty may be overcome to
a certain extent. Among the external conditions of these processes some are directly accessible to measurement (the time,
the number of repetitions). They may be employed in getting numerical values indirectly where that would not have been possible
directly. We must not wait until the series of ideas committed to memory return to consciousness of themselves, but we must
meet them halfway and renew them to such an extent that they may just be reproduced without error. The work requisite for
this under certain conditions I take experimentally as a measure of the influence of these conditions; the differences in
the work which appear with a change of conditions I interpret as a measure of the influence of that change.
Whether the first difficulty, the establishment of stable experimental conditions, may also be overcome satisfactorily
cannot be decided a priori. Experiments must be made under conditions as far as possible the same, to see whether the
results, which will probably deviate from one another when taken separately, will furnish constant mean values when collected
to form larger groups. However, taken by itself, this is not sufficient to enable us to utilise such numerical results for
the establishment of numerical relations of dependence in the natural science sense. Statistics is concerned with a great
mass of constant mean values that do not at all arise from the frequent repetition of an ideally frequent occurrence and therefore
cannot favor further insight into it. Such is the great complexity of our mental life that it is not possible to deny that
constant mean values, when obtained, are of the nature of such statistical constants. To test that, I examine the distribution
of the separate numbers represented in an average value. If it corresponds to the distribution found everywhere in natural
science, where repeated observation of the same occurrence furnishes different separate values, I suppose -- tentatively again
-- that the repeatedly examined psychical process in question occurred each time under conditions sufficiently similar for
our purposes. This supposition is not compulsory, but is very probable. If it is wrong, the continuation of experimentation
will presumably teach this by itself: the questions put from different points of view will lead to contradictory results.
Section 10. The Probable Error
The quantity which measures the compactness of the observed values obtained in any given case and which makes the formula
which represents their distribution a definite one may, as has already been stated, be chosen differently. I use the so-called
"probable error" (P.E.) -- i.e., that deviation above and below the mean value which is just as often exceeded by the
separate values as not reached by them, and which, therefore, between its positive and negative limits, includes just half
of all the observational results symmetrically arranged around the mean value. As is evident from the definition these values
can be obtained from the results by simple enumeration; it is done more accurately by a theoretically based calculation.
If now this calculation is tried out tentatively for any group of observations, a grouping of these values according to
the "law of errors" is recognised by the fact that between the sub-multiples and the multiples of the empirically calculated
probable error there are obtained as many separate measures symmetrically arranged about a central value as the theory requires.
According to this out of 1,000 observations there should be:
|
Within the limits |
Number of separate measures |
|
± 1/10 P.E. |
54 |
|
± 1/6 P.E. |
89.5 |
|
± 1/4 P.E. |
134 |
|
± 1/2 P.E. |
264 |
|
± [sic] P.E. |
500 |
|
± 1 1/2 P.E. |
688 |
|
± 2 P.E. |
823 |
|
± 2 1/2 P.E. |
908 |
|
± 3 P.E. |
957 |
|
± 4 P.E. |
993 |
If this conformity exists in a sufficient degree, then the mere statement of the probable error suffices to characterise
the arrangement of all the observed values, and at the same time its quantity gives a serviceable measure for the compactness
of the distribution around the central value-i.e., for its exactness and trustworthiness.
As we have spoken of the probable error of the separate observations, (P.E.o), so can we also speak of the probable
error of the measures of the central tendency, or mean values, (P.E.m). This describes in similar fashion the grouping
which would arise for the separate mean values if the observation of the same phenomenon were repeated very many times and
each time an equally great number of observations were combined into a central value. It furnishes a brief but sufficient
characterisation of the fluctuations of the mean values resulting from repeated observations, and along with it a measure
of the security and the trustworthiness of the results already found.
The P.E.m is accordingly in general included in what follows. How it is found by calculation, again, cannot
be explained here; suffice it that what it means be clear. It tells us, then, that, on the basis of the character of the total
observations from which a mean value has just been obtained, it may be expected with a probability of 1 to 1 [sic]
that the latter value departs from the presumably correct average by not more at the most than the amount of its probable
error. By the presumably correct average we mean that one which would have been obtained if the observations had been indefinitely
repeated. A larger deviation than this becomes improbable in the mathematical sense -- i.e., there is a greater probability
against it than for it. And, as a glance at the accompanying table shows us, the improbability of larger deviations increases
with extreme rapidity as their size increases. The probability that the obtained average should deviate from the true one
by more than 2 1/2 times the probable error is only 92 to 908, therefore about 1/10; the probability for its exceeding
four times the probable error is very slight, 7 to 993 (1 to 142).
Footnotes
[1] The numbers representing the births of boys and girls respectively, as derived from the total number of births, are said
to group themselves in very close correspondence with the law of errors. But in this case it is for this very reason probable
that they arise from a homogeneous combination of physiological causes aiming so to speak at the creation of a well determined
relation. (See Lexis, Zur Theorie der Massenerscheinungen in der menschlichen Gesellschaft, p. 64 and elsewhere.)
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER III
THE METHOD OF INVESTIGATION
Section 11. Series of Nonsense Syllables
In order to test practically, although only for a limited field, a way of penetrating more deeply into memory processes
-- and it is to these that the preceding considerations have been directed -- I have hit upon the following method.
Out of the simple consonants of the alphabet and our eleven vowels and diphthongs all possible syllables of a certain sort
were constructed, a vowel sound being placed between two consonants.[1]
These syllables, about 2,300 in number, were mixed together and then drawn out by chance and used to construct series of
different lengths, several of which each time formed the material for a test.[2]
At the beginning a few rules were observed to prevent, in the construction of the syllables, too immediate repetition of
similar sounds, but these were not strictly adhered to. Later they were abandoned and the matter left to chance. The syllables
used each time were carefully laid aside till the whole number had been used, then they were mixed together and used again.
The aim of the tests carried on with these syllable series was, by means of repeated audible perusal of the separate series,
to so impress them that immediately afterward they could voluntarily be reproduced. This aim was considered attained when,
the initial syllable being given, a series could be recited at the first attempt, without hesitation, at a certain rate, and
with the consciousness of being correct.
Section 12. Advantages of the Material
The nonsense material, just described, offers many advantages, in part because of this very lack of meaning. First of all,
it is relatively simple and relatively homogeneous. In the case of the material nearest at hand, namely poetry or prose, the
content is now narrative in style, now descriptive, or now reflective; it contains now a phrase that is pathetic, now one
that is humorous; its metaphors are sometimes beautiful, sometimes harsh; its rhythm is sometimes smooth and sometimes rough.
There is thus brought into play a multiplicity of influences which change without regularity and are therefore disturbing.
Such are associations which dart here and there, different degrees of interest, lines of verse recalled because of their striking
quality or their beauty, and the like. All this is avoided with our syllables. Among many thousand combinations there occur
scarcely a few dozen that have a meaning and among these there are again only a few whose meaning was realised while they
were being memorised.
However, the simplicity and homogeneity of the material must not be overestimated. It is still far from ideal. The learning
of the syllables calls into play the three sensory fields, sight, hearing and the muscle sense of the organs of speech. And
although the part that each of these senses plays is well limited and always similar in kind, a certain complication of the
results must still be anticipated because of their combined action. Again, to particularise, the homogeneity of the series
of syllables falls considerably short of what might be expected of it. These series exhibit very important and almost incomprehensible
variations as to the ease or difficulty with which they are learned. It even appears from this point of view as if the differences
between sense and nonsense material were not nearly so great as one would be inclined a priori to imagine. At
least I found in the case of learning by heart a few cantos from Byron's "Don Juan" no greater range of distribution of the
separate numerical measures than in the case of a series of nonsense syllables in the learning of which an approximately equal
time had been spent. In the former case the innumerable disturbing influences mentioned above seem to have compensated each
other in producing a certain intermediate effect; whereas in the latter case the predisposition, due to the influence of the
mother tongue, for certain combinations of letters and syllables must be a very heterogeneous one.
More indubitable are the advantages of our material in two other respects. In the first place it permits an inexhaustible
amount of new combinations of quite homogeneous character, while different poems, different prose pieces always have something
incomparable. It also makes possible a quantitative variation which is adequate and certain; whereas to break off before the
end or to begin in the middle of the verse or the sentence leads to new complications because of various and unavoidable disturbances
of the meaning.
Series of numbers, which I also tried, appeared impracticable for the more thorough tests. Their fundamental elements were
too small in number and therefore too easily exhausted.
Section 13. Establishment of the Most Constant Experimental Conditions Possible
The following rules were made for the process of memorising.
1. The separate series were always read through completely from beginning to end; they were not learned in separate parts
which were then joined together; neither were especially difficult parts detached and repeated more frequently. There was
a perfectly free interchange between the reading and the occasionally necessary tests of the capacity to reproduce by heart.
For the latter there was an important rule to the effect that upon hesitation the rest of the series was to be read through
to the end before beginning it again.
2. The reading and the recitation of the series took place at a constant rate, that of 150 strokes per minute. A clockwork
metronome placed at some distance was at first used to regulate the rate; but very soon the ticking of a watch was substituted,
that being much simpler and less disturbing to the attention. The mechanism of escapement of most watches swings 300 times
per minute.
3. Since it is practically impossible to speak continuously without variation of accent, the following method was adopted
to avoid irregular variations: either three or four syllables were united into a measure, and thus either the 1st, 4th, 7th,
or the 1st, 5th, 9th ... syllables were pronounced with a slight accent. Stressing of the voice was otherwise, as far as possible,
avoided.
4. After the learning of each separate series a pause of 15 seconds was made, and used for the tabulation of results. Then
the following series of the same test was immediately taken up.
5. During the process of learning, the purpose of reaching the desired goal as soon as possible was kept in mind as much
as was feasible. Thus, to the limited degree to which conscious resolve is of influence here, the attempt was made to keep
the attention concentrated on the tiresome task and its purpose. It goes without saying that care was taken to keep away all
outer disturbances in order to make possible the attainment of this aim. The smaller distractions caused by carrying on the
test in various surroundings were also avoided as far as that could be done.
6. There was no attempt to connect the nonsense syllables by the invention of special associations of the mnemotechnik
[sic] type; learning was carried on solely by the influence of the mere repetitions upon the natural memory. As I do not possess
the least practical knowledge of the mnemotechnical devices, the fulfillment of this condition offered no difficulty to me.
7. Finally and chiefly, care was taken that the objective conditions of life during the period of the tests were so controlled
as to eliminate too great changes or irregularities. Of course, since the tests extended over many months, this was possible
only to a limited extent. But, even so, the attempt was made to conduct, under as similar conditions of life as possible,
those tests the results of which were to be directly compared. In particular the activity immediately preceding the test was
kept as constant in character as was possible. Since the mental as well as the physical condition of man is subject to an
evident periodicity of 24 hours, it was taken for granted that like experimental conditions are obtainable only at like times
of day. However, in order to carry out more than one test in a given day, different experiments were occasionally carried
on together at different times of day. When too great changes in the outer and inner life occurred, the tests were discontinued
for a length of time. Their resumption was preceded by some days of renewed training varying according to the length of the
interruption.
Section 14. Sources of Error
The guiding point of view in the selection of material and in determining the rules for its employment was, as is evident,
the attempt to simplify as far as possible, and to keep as constant as possible, the conditions under which the activity to
be observed, that of memory, came into play. Naturally the better one succeeds in this attempt the more does he withdraw from
the complicated and changing conditions under which this activity takes place in ordinary life and under which it is of importance
to us. But that is no objection to the method. The freely falling body and the frictionless machine, etc., with which physics
deals, are also only abstractions when compared with the actual happenings in nature which are of import to us. We can almost
nowhere get a direct knowledge of the complicated and the real, but must get at them in roundabout ways by successive combinations
of experiences, each of which is obtained in artificial, experimental cases, rarely or never furnished in this form by nature.
Meanwhile the fact that the connection with the activity of memory in ordinary life is for the moment lost is of less importance
than the reverse, namely, that this connection with the complications and fluctuations of life is necessarily still a too
close one. The struggle to attain the most simple and uniform conditions possible at numerous points naturally encounters
obstacles that are rooted in the nature of the case and which thwart the attempt. The unavoidable dissimilarity of the material
and the equally unavoidable irregularity of the external conditions have already been touched upon. I pass next to two other
unsurmountable [sic] sources of difficulty.
By means of the successive repetitions the series are, so to speak, raised to ever higher levels. The natural assumption
would be that at the moment when they could for the first time be reproduced by heart the level thus attained would always
be the same. If this were the case, i.e., if this characteristic first reproduction were everywhere an invariable objective
sign of an equally invariable fixedness of the series, it would be of real value to us. This, however, is not actually the
case. The inner conditions of the separate series at the moment of the first possible reproduction are not always the same,
and the most that can be assumed is that in the case of these different series these conditions always oscillate about the
same degree of inner surety. This is clearly seen if the learning and repeating of the series is continued after that first
spontaneous reproduction of the series has been attained. As a general thing the capacity for voluntary reproduction persists
after it has once been reached. In numerous cases, however, it disappears immediately after its first appearance, and is regained
only after several further repetitions. This proves that the predisposition for memorising the series, irrespective of their
differences of a larger sort according to the time of day, to the objective and subjective conditions, etc., is subject to
small variations of short duration, whether they be called oscillations of attention or something else. If, at the very instant
when the material to be memorised has almost reached the desired degree of surety, a chance moment of especial mental clearness
occurs, then the series is caught on the wing as it were, often to the learner's surprise; but the series cannot long be retained.
By the occurrence of a moment of special dullness, on the other hand, the first errorless reproduction is postponed for a
while, although the learner feels that he really is master of the thing and wonders at the constantly recurring hesitations.
In the former case, in spite of the homogeneity of the external conditions, the first errorless reproduction is reached at
a point a little below the level of retention normally connected with it. In the latter case it is reached at a point a little
above that level. As was said before, the most plausible conjecture to make in this connection is that these deviations will
compensate each other in the case of large groups.
Of the other source of error, I can only say that it may occur and that, when it does, it is a source of great danger.
I mean the secret influence of theories and opinions which are in the process of formation. An investigation usually starts
out with definite presuppositions as to what the results will be. But if this is not the case at the start, such presuppositions
form gradually in case the experimenter is obliged to work alone. For it is impossible to carry on the investigations for
any length of time without taking notice of the results. The experimenter must know whether the problem has been properly
formulated or whether it needs completion or correction. The fluctuations of the results must be controlled in order that
the separate observations may be continued long enough to give to the mean value the certainty necessary for the purpose in
hand. Consequently it is unavoidable that, after the observation of the numerical results, suppositions should arise as to
general principles which are concealed in them and which occasionally give hints as to their presence. As the investigations
are carried further, these suppositions, as well as those present at the beginning, constitute a complicating factor which
probably has a definite influence upon the subsequent results. It goes without saying that what I have in mind is not any
consciously recognised influence but something similar to that which takes place when one tries to be very unprejudiced or
to rid one's self of a thought and by that very attempt fosters that thought or prejudice. The results are met half way with
an anticipatory knowledge, with a kind of expectation. Simply for the experimenter to say to himself that such anticipations
must not be allowed to alter the impartial character of the investigation will not by itself bring about that result. On the
contrary, they do remain and play a rôle in determining the whole inner attitude. According as the subject notices that these
anticipations are confirmed or not confirmed (and in general he notices this during the learning), he will feel, if only in
a slight degree, a sort of pleasure or surprise. And would you not expect that, in spite of the greatest conscientiousness,
the surprise felt by the subject over especially startling deviations, whether positive or negative, would result, without
any volition on his part, in a slight change in attitude? Would he not be likely to exert himself a little more here and to
relax a little more there than would have been the case had he had no knowledge or presupposition concerning the probable
numerical value of the results? I cannot assert that this is always or even frequently the case, since we are not here concerned
with things that can be directly observed, and since numerous results in which such secret warping of the truth might be expected
show evident independence of it. All I can say is, we must expect something of the sort from our general knowledge of human
nature, and in any investigations in which the inner attitude is of very great importance, as for example in experiments on
sense perception, we must give special heed to its misleading influence.
It is evident how this influence in general makes itself felt. With average values it would tend to level the extremes;
where especially large or small numbers are expected it would tend to further increase or decrease the values. This influence
can only be avoided with certainty when the tests are made by two persons working together, one of whom acts as subject for
a certain time without raising any questions concerning the purpose or the result of the investigations. Otherwise help can
be obtained only by roundabout methods, and then, probably, only to a limited extent. The subject, as I myself always did,
can conceal from himself as long as possible the exact results. The investigation can be extended in such a way that the upper
limits of the variables in question are attained. In this way, whatever warping of the truth takes place becomes relatively
more difficult and unimportant. Finally, the subject can propose many problems which will appear to be independent of each
other in the hope that, as a result, the true relation of the interconnected mental processes will break its way through.
To what extent the sources of error mentioned have affected the results given below naturally cannot be exactly determined.
The absolute value of the numbers will doubtless be frequently influenced by them, but as the purpose of the tests could never
have been the precise determination of absolute values, but rather the attainment of comparative results (especially in the
numerical sense) and relatively still more general results, there is no reason for too great anxiety. In one important case
(sec. 38) I could directly convince myself that the exclusion of all knowledge concerning the character of the results brought
about no change; in another case where I myself could not eliminate a doubt I called especial attention to it. In any case
he who is inclined a priori to estimate very highly the unconscious influence of secret wishes on the total mental
attitude will also have to take into consideration that the secret wish to find objective truth and not with disproportionate
toil to place the creation of his own fancy upon the feet of clay -- that this wish, I say, may also claim a place in the
complicated mechanism of these possible influences.
Section 15. Measurement of Work Required
The number of repetitions which were necessary for memorising a series up to the first possible reproduction was not originally
determined by counting, but indirectly by measuring in seconds the time that was required to memorise it. My purpose was in
this way to avoid the distraction necessarily connected with counting; and I could assume that there was a proportional relation
existing between the times and the number of repetitions occurring at any time in a definite rhythm. We could scarcely expect
this proportionality to be perfect, since, when only the time is measured, the moments of hesitation and reflection are included,
which is not true when the repetitions are counted. Difficult series in which hesitation will occur relatively more frequently,
will, by the method of time measurement, get comparatively greater numbers, the easier series will get comparatively smaller
numbers than when the repetitions are counted. But with larger groups of series a tolerably equal distribution of difficult
and equal series may be taken for granted. Consequently the deviations from proportionality will compensate themselves in
a similar manner in the case of each group.
When, for certain tests, the direct counting of the repetitions became necessary, I proceeded in the following manner.
Little wooden buttons measuring about 14 mms. in diameter and 4 mms. at their greatest thickness were strung on a cord which
would permit of easy displacement and yet heavy enough to prevent accidental slipping. Each tenth piece was black; the others
had their natural color. During the memorisation the cord was held in the hand and at each new repetition a piece was displaced
some centimeters from left to right. When the series could be recited, a glance at the cord, since it was divided into tens,
was enough to ascertain the number of repetitions that had been necessary. The manipulation required so little attention that
in the mean values of the time used (which was always tabulated at the same time) no lengthening could be noted as compared
with earlier tests.
By means of this simultaneous measurement of time and repetitions incidental opportunity was afforded for verifying and
more accurately defining that which had been foreseen and which has just been explained with regard to their interrelation.
When the prescribed rhythm of 150 strokes per minute was precisely maintained, each syllable would take 0.4 second; and when
the simple reading of the series was interrupted by attempts to recite it by heart, the unavoidable hesitations would lengthen
the time by small but fairly uniform amounts. This, however, did not hold true with any exactness; on the contrary, the following
modifications appeared.
When the direct reading of the series predominated, a certain forcing, an acceleration of the rhythm, occurred which, without
coming to consciousness, on the whole lowered the time for each syllable below the standard of 0.4 sec.
When there was interchange between reading and reciting, however, the lengthening of the time was not in general constant,
but was greater with the longer series. In this case, since the difficulty increases very rapidly with increasing length of
the series, there occurs a slowing of the tempo, again involuntary and not directly noticeable. Both are illustrated by the
following table.
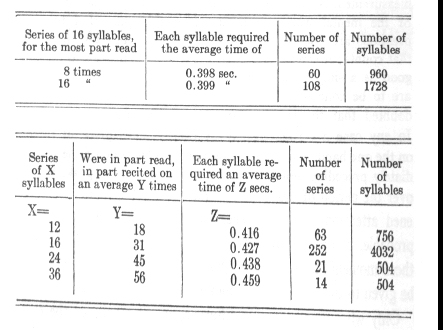
As soon as this direction of deviation from exact proportionality was noticed there appeared in the learning a certain
conscious reaction against it.
Finally, it appeared that the probable error of the time measurements was somewhat larger than that of the repetitions.
This relation is quite intelligible in the light of the explanations given above. In the case of the time measurements the
larger values, which naturally occurred with the more difficult series, were relatively somewhat greater than in the case
of the number of repetitions, because relatively they were for the most part lengthened by the hesitations; conversely, the
smaller times were necessarily somewhat smaller relatively than the number of repetitions, because in general they corresponded
to the easier series. The distribution of the values in the case of the times is therefore greater than that of the values
in the case of the repetitions.
The differences between the two methods of reckoning are, as is readily seen, sufficiently large to lead to different results
in the case of investigations seeking a high degree of exactness. That is not the case with the results as yet obtained; it
is therefore immaterial whether the number of seconds is used or that of the repetitions.
Decision cannot be given a priori as to which method of measurement is more correct-- i.e., is the more adequate
measure of the mental work expended. It can be said that the impressions are due entirely to the repetitions, they are the
thing that counts; it can be said that a hesitating repetition is just as good as a simple fluent reproduction of the line,
and that both are to be counted equally. But on the other hand it may be doubted that the moments of recollection are merely
a loss, In ,any case a certain display of energy takes place in them: on the one hand, a very rapid additional recollection
of the immediately preceding words occurs, a new start, so to speak, to get over the period of hesitation; on the other hand,
there is heightened attention to the passages following. If with this, as is probable, a firmer memorisation of the series
takes place, then these moments have a claim upon consideration which can only be given to them through the measurement of
the times.
Only when a considerable difference in the results of the two kinds of tabulation appears will it be possible to give one
the preference over the other. That one will then be chosen which gives the simpler formulation of the result in question.
Section 16. Periods of the Tests
The tests were made in two periods, in the years 1879-80 and 1883-84, and extended each over more than a year. During a
long time preliminary experiments of a similar nature had preceded the definite tests of the first period, so that, for all
results communicated, the time of increasing skill may be considered as past. At the beginning of the second period I was
careful to give myself renewed training. This temporal distribution of the tests with a separating interval of more than three
years gives the desired possibility of a certain mutual control of most of the results. Frankly, the tests of the two periods
are not strictly comparable. In the case of the tests of the first period, in order to limit the significance of the first
fleeting grasp[3] of the series in moments of special concentration, it was decided to study the series until two successive faultless reproductions
were possible. Later I abandoned this method, which only incompletely accomplished its purpose, and kept to the first fluent
reproduction. The earlier method evidently in many cases resulted in a somewhat longer period of learning. In addition there
was a difference in the hours of the day appointed for the tests. Those of the later period all occurred in the afternoon
hours between one and three o'clock; those of the earlier period were unequally divided between the hours of 10-11 A.M., 11-12
A.M., and 6-8 P.M., which for the sake of brevity I shall designate A, B, and C.
Footnotes
[1] The vowel sounds employed were a, e, i, o, u, ä ö, ü, au, ei, eu. For the beginning of the syllables the following consonants
were employed: b, d, f g, h, j, k, l, m, n, p, r, s, (= sz), t, w and in addition ch, sch, soft s, and the French j (19 altogether);
for the end of the syllables f, k, l, m, n, p, r, s, (= sz) t, ch, sch (11 altogether). For the final sound fewer consonants
were employed than for the initial sound, because a German tongue even after several years practise in foreign languages does
not quite accustom itself to the correct pronunciation of the mediae at the end. For the same reason I refrained from the
use of other foreign sounds although I tried at first to use them for the sake of enriching the material.
[2] I shall retain in what follows the designations employed above and call a group of several syllable series
or a single series a "test." A number of "tests" I shall speak of as a "test series" or a "group of tests."
[3] Described in sec. 14.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER IV
THE UTILITY OF THE AVERAGES OBTAINED
Section 17. Grouping of the Results of the Tests
The first question which awaits an answer from the investigations carried out in the manner described is, as explained
in sections 7 and 8, that of the nature of the averages obtained. Are the lengths of time required for memorising series of
a certain length, under conditions as nearly identical as possible, grouped in such a way that we may be justified in considering
their average values as measures in the sense of physical science, or are they not?
If the tests are made in the way described above, namely, so that several series are always memorised in immediate succession,
such a type of grouping of the time records could scarcely be expected. For, as the time devoted to learning at a given sitting
becomes extended, certain variable conditions in the separate series come into play, the fluctuations of which we could not
very well expect, from what we know of their nature, to be distributed symmetrically around a mean value. Accordingly the
grouping of the results must be an asymmetrical one and cannot correspond to the "law of error." Such conditions are the fluctuations
of attention and the decreasing mental freshness, which, at first very quickly and then more and more slowly, gives way to
a certain mental fatigue. There are no limits, so to speak, to the slowing down of the learning processes caused by unusual
distractions; as a result of these the time for learning a series may occasionally be increased to double that of its average
value or more. The opposite effect, that of an unusual exertion, cannot in the very nature of the case overstep a certain
limit. It can never reduce the learning time to zero.
If, however, groups of series equal in number and learned in immediate succession are taken, these disturbing influences
may be considered to have disappeared or practically so. The decrease in mental vigour in one group will be practically the
same as that in another. The positive and negative fluctuations of attention which under like conditions occur during a quarter
or half hour are approximately the same from day to day. All that is necessary to ask, then, is: Do the times necessary for
learning equal groups of series exhibit the desired distribution?
I can answer this question in the affirmative with sufficient certainty. The two longest series, obtained under conditions
similar to each other, which I possess, are, to be sure, not large in the above-mentioned theoretical sense; they suffer,
moreover, from the disadvantage that they originated at times separated by comparatively long intervals during which there
were necessarily many changes in the conditions. In spite of this, their grouping comes as near as could be expected to the
one demanded by the theory.
The first test series taken during the years 1879-80 comprises 92 tests. Each test consisted in memorising eight series
of 13 syllables each, which process of learning was continued until two reproductions of each series were possible. The time
required for all eight series taken together including the time for the two reproductions (but of course not for the pauses,
see p. 25, 4) amounted to an average of 1,112 seconds with a probable error of observation of ± 76.
The fluctuations of the results were, therefore, very significant: only half of the numbers obtained fell between the limits
1,036 and 1,188, the other half was distributed above and below these limits. In detail the grouping of the numbers is as
follows:
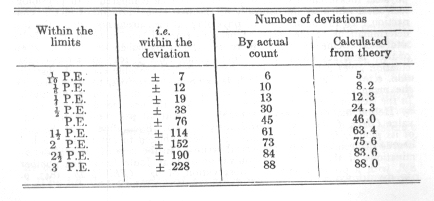
In the interval, 1/4 P.E. to 1/2 P.E., there occurs a slight piling up of values which is compensated for by a greater
lack in the succeeding interval, 1/2 P.E. to P.E. Apart from this, the correspondence between the calculated and the actual
results is satisfactory. The symmetry of the distribution leaves something to be desired. The values below the average preponderate
a little in number, those above preponderate a little in amount of deviation: only two of the largest eight deviations are
below the mean value. The influence of attention referred to above, the fluctuations of which in the separate series show
greater deviations toward the upper limit than toward the lower, has not, therefore, been quite compensated by the combination
of several series.
The correctness of the observations and the correspondence of their distributions with the one theoretically demanded are
greatly improved in the second large series of tests. The latter comprises the results of 84 series of tests taken during
the years 1883-84. Each test consisted in memorising six series of 16 syllables each, carried on in each case to the first
errorless reproduction. The whole time necessary for this amounted to 1,261 seconds with the probable error of observation
of ± 48.4 -- i.e., half of all the 84 numbers fell within the limits 1,213-1,309. The exactness
of ths observations thus had greatly increased as compared with the former series of tests :[1]
The interval included by the probable error amounts to only 7 1/2 per cent of the mean values as against 14 per cent in
the earlier tests. In detail the numbers are distributed as follows:
The symmetry of distribution is here satisfactorily maintained apart from the numbers, which are unimportant on account
of their smallness.
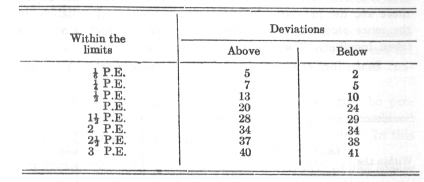
The deviation which is greatest absolutely is toward the lower limit.
If several of our series of syllables were combined into groups and then memorised separately, the length of time necessary
to memorise a whole group varied greatly, to be sure, when repeated tests were taken; but, in spite of this, when taken as
a whole they varied in a manner similar to that of the measures of the ideally homogeneous processes of natural science, which
also vary from each other. So, at least in experimental fashion, it is allowable to use the mean values obtained from the
numerical results for the various tests in order to establish the existence of causal relations just as natural science does
that by means of its constants.
The number of series of syllables which is to be combined into a single group, or test, is naturally indeterminate. It
must be expected, however, that as the number increases, the correspondence between the distribution of the times actually
found and those calculated in accordance with the law of errors will be greater. In practice the attempt will be made to increase
the number to such a point that further increase and the closer correspondence resulting will no longer compensate for the
time required. If the number of the series in a given test is lessened, the desired correspondence will also presumably decrease.
However, it is desirable that even then the approximation to the theoretically demanded distribution remain perceptible.
Even this requirement is fulfilled by the numerical values obtained. In the two largest series of tests just described,
I have examined the varying length of time necessary for the memorisation of the first half of each test. In the older series,
these are the periods required by each 4 series of syllables, in the more recent series the periods required by each 3 of
them taken together. The results are as follows:
1. In the former series: mean value (m) = 533 (P.E.o) = ± 51.
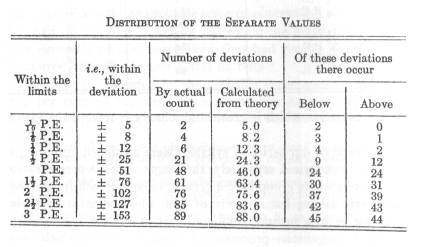
2. In the later series: m = 620, P.E.o = ± 44.
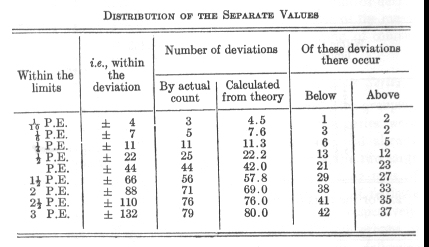
By both tables the supposition mentioned above of the existence of a less perfect but still perceptible correspondence
between the observed and calculated distribution of the numbers is well confirmed.
Exactly the same approximate correspondence must be presupposed if, instead of decreasing the number of series combined
into a test, the total number of tests is made smaller. In this case also I will add some confirmatory summaries.
I possess two long test series, made at the time of the earlier tests, which were obtained under the same conditions as
the above mentioned series but at the later times of the day, B. and C.
One of these, B, comprised 39 tests of 6 series each, the other, C, 38 tests of 8 series each, each series containing 13
syllables. The results obtained were as follows:
- For the tests at time B: m = 871, P.E.o = ± 63.
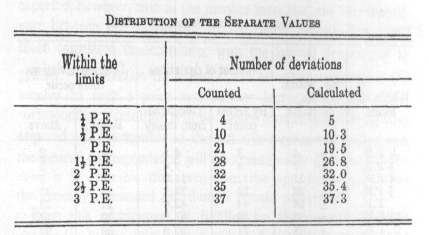
- For the test of time C: m = 1,258, P.E.o = ± 60.
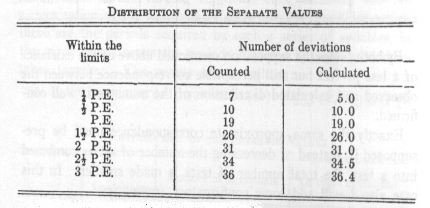
In addition I mention a series of only twenty tests, with which I shall conclude this summary. Each test consisted of the
learning of eight separate series of thirteen syllables each, which had been memorised once one month before. The average
was in this case 892 seconds with a probable error of observation of 54. The single values were grouped as follows:

Although the number of the tests was so small, the accordance between the calculation by theory and the actual count of
deviations is in all these cases so close that the usefulness of the mean values will be admitted, the wide limits of error
being, of course, taken into consideration.
Section 18. Grouping of the Results of the Separate Series
The previously mentioned hypotheses concerning the grouping of the times necessary for learning the separate series were
naturally not merely theoretical suppositions, but had already been confirmed by the groupings actually found. The two large
series of tests mentioned above, one consisting of 92 tests of eight single series each, and the other of 84
tests of 6 single series each, thus giving 736 and 504 separate values respectively, afford a sufficiently broad basis for
judgment. Both groups of numbers, and both in the same way, show the following peculiarities:
1. The distribution of the arithmetical values above their mean is considerably looser and extends farther than below the
mean. The most extreme values above lie 2 times and 1.8 times, respectively, as far from the mean as the most distant of those
below.
2. As a result of this dominance by the higher numbers the mean is displaced upward from the region of the densest distribution,
and as a result the deviations below get the preponderance in number. There occur respectively 404 and 266 deviations below
as against 329 and 230 above.
3. The number of deviations from the region of densest distribution towards both limits does not decrease uniformly --
as one would be very much inclined to expect from the relatively large numbers combined -- but several maxima and minima of
density are distinctly noticeable. Therefore constant sources of error were at work in the production of the separate values
-- i.e., in the memorisation of the separate series. These resulted on the one hand in an unsymmetrical distribution
of the numbers, and on the other hand in an accumulation of them in certain regions. In accordance with the investigations
already presented in this chapter, it can only be supposed that these influences compensated each other when the values of
several series learned in succession were combined.
I have already mentioned as the probable cause of this unsymmetrical distribution the peculiar variations in the effect
of high degrees of concentration of attention and distraction. It would naturally be supposed that the position of the separate
series within each test is the cause of the repeated piling up of values on each side of the average. If, in the case of a
large test-series, the values are summed up for the first, the second, and third series, etc., and the average of each is
taken, these average values vary greatly, as might be expected. The separate values are grouped about their mean with only
tolerable approximation to the law of error, but yet they are, on the whole, distributed most densely in its region, and these
separate regions of dense distribution must of course appear in the total result. 
The following may be added by way of supplement: on account of the mental fatigue which increases gradually during the
course of a test-series the mean values ought to increase with the number of the series; but this does not prove to be the
case.
Only in one case have I been able to notice anything corresponding to this hypothesis, namely, in the large and therefore
important series of 92 tests consisting of eight series of 13 syllables each. In this case the mean values for the learning
of the 92 first series, the 92 second series, etc., were found to be 105, 140, 142, 146, 148, 140 seconds, the relative lengths
of which Fig 2 exhibits. For all the rest of the cases which I investigated the typical fact is, on the contrary, rather suc
ha course of the numbers as was true in the case of the series of 84 tests of six series of 16 syllables each and as is shown
in Fig. 3. 
The mean values here were 191, 224, 206, 218, 210, 213 seconds. They start in, as may be seen, considerably below the average,
but rise immediately to a height which is not again reached in the further course of the test, and they then oscillate rather
decidedly. An analogous course is shown by the numbers in the 7 tests of nine 12-syllable series, namely: 71, 90, 98, 87,
98, 90, 101, 86, 69 (Fig. 4).
Furthermore the values for 39 tests of six series of 13 syllables each obtained in time B were as follows: 118, 150, 158,
147, 155, 144 (Fig. 5 lower curve).
Those for 38 tests with eight 13 syllable series of time C were 139,159,167, 168, 160, 150,162,153 (Fig. 5 upper
curve). 
Finally the numbers obtained from seven tests with six stanzas of Byron's "Don Juan" were: 189, 219, 171, 204 183, 229.
Even in the case of the first mentioned contradictory group of tests a grouping of the separate mean values harmonising
with the normal one occurs if, instead of all the 92 tests being taken into consideration at once, they are divided
into several parts -- i.e., if tests are combined which were taken at about the same time and under about the same
conditions.
The conclusion cannot be drawn from these numerical results that the mental fatigue which gradually increased during the
twenty minute duration of the tests did not exert any influence. 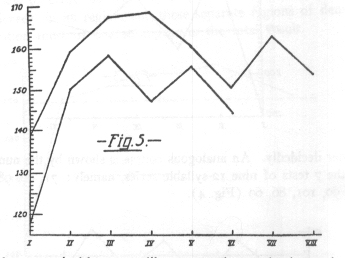
It can only be said that the supposed influence of the latter upon the numbers is far outweighed by another tendency which
would not a priori be so readily suspected, namely the tendency of comparatively low values to be followed by comparatively
high ones and vice versa. There seems to exist a kind of periodical oscillation of mental receptivity or attention in connection
with which the increasing fatigue expresses itself by fluctuations around a median position which is gradually displaced.[2]
After orienting ourselves thus concerning the nature and value of the numerical results gained from the complete memorisations,
we shall now turn to the real purpose of the investigation, namely the numerical description of causal relations.
Footnotes
[1] Of course, the exactness obtained here cannot stand comparison with physical measurements, but it can very well be compared
with physiological ones, which would naturally be the first to be thought of in this connection. To the most exact of physiological
measurements belong the last determinations of the speed of nervous transmission made by Helmholtz and Baxt. One record of
these researches published as an illustration of their accuracy (Mon. Ber, d. Berl. Akad. 1870, S. 191) after proper calculation
gives a mean value of 4.268 with the probable error of observation, 0.101. The interval it includes amounts, therefore, to
5 per cent of the mean value. All former determinations are much more inaccurate. In the case of the most accurate test-series
of the first measurements made by Helmholtz, that interval amounts to about 50 per cent of the mean value (Arch. f. Anat.
u.. Physiol. 1850, S. 340). Even Physics, in the case of its pioneer investigations, has often been obliged to put up
with a less degree of accuracy in its numerical results. In the case of his first determinations of the mechanical equivalent
of heat Joule found the number 838, with a probable error of observation of 97. (Phil. Mag., 1843, p. 435 ff.)
[2] If it should ever become a matter of interest the attempt might be made to define numerically the different
effects of that tendency in different cases. For the probable errors of observation for the numerical values of series-groups
afford a measure for the influence of accidental disturbances to which the memorisation is daily exposed. If now the learning
of the separate series in general were exposed to the same of similar variations of condition as occur from test to test,
then according to the fundamental principles of the theory of errors, a probable error of observation calculated directly
from the spearate values would relate itself to the one just mentioned as 1 to [the square root of] n, where "n" denotes the
number of separate series combined into a test. If however, as is the case here, special influences assert themselves during
the memorisation of these separate series, and if such influences tend to separate the values further than other variations
of conditions would do, the " P.E.0 "calculated from the separate values must turn out somewhat too great, and
the just mentioned proportion consequently too small, and the stronger the influences are, the more must this be the case.
An examination of the actual relations is, to be sure, a little difficult, but fully confirms the statements. In the 84
tests, consisting of six series of 16 syllables each, the [square root of] n = 2.45. We found 48.4 to be the probable error
of observation of the 84 tests. The probable error of the 504 separate values is 31.6. The quotient 31.6: 48.4 is 1.53; therefore
not quite 2/3 of the value of [the square root of] n.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER V
RAPIDITY OF LEARNING SERIES OF SYLLABLES AS A FUNCTION OF THEIR LENGTH
Section 19. Tests Belonging to the Later Period
It is sufficiently well known that the memorisation of a series of ideas that is to be reproduced at a later time is more
difficult, the longer the series is. That is, the memorisation not only requires more time taken by itself, because each repetition
lasts longer, but it also requires more time relatively because an increased number of repetitions becomes necessary. Six
verses of a poem require for learning not only three times as much time as two but considerably more than that.
I did not investigate especially this relation of dependence, which of course becomes evident also in the first possible
reproduction of series of nonsense syllables, but incidentally I obtained a few numerical values for it which are worth putting
down, although they do not show particularly interesting relations.
The series in question comprised (in the case of the tests of the year 1883-84), 12, 16, 24, or 36 syllables each, and
9, 6, 3, or 2 series were each time combined into a test.
For the number of repetitions necessary in these cases to memorise the series up to the first errorless reproduction (and
including it) the following numerical results were found:

In order to make the number of repetitions comparable it is necessary, so to speak, to reduce them to a common denominator
and to divide them each time by the number of the series. In this way it is found out how many repetitions relatively were
necessary to learn by heart the single series, which differ from each other only in the number of syllables, and which each
time had been taken together with as many others of the same kind as would make the duration of the whole test from fifteen
to thirty minutes.[1]
However, a conclusion can be drawn from the figures from the standpoint of decrease in number of syllables The question
can he asked: What number of syllables can be correctly recited after only one reading? For me the number is usually seven.
Indeed I have often succeeded in reproducing eight syllables, but this has happened only at the beginning of the tests and
in a decided minority of the cases. In the case of six syllables on the other hand a mistake almost never occurs; with them,
therefore, a single attentive reading involves an unnecessarily large expenditure of energy for an immediately following reproduction.
If this latter pair of values is added, the required division made, and the last faultless reproduction subtracted as not
necessary for the learning, then the following table results.
|
Number of syllables
in a series |
Number of repetitions necessary for first errorless reproduction (exclusive of it) |
Probable
error |
|
7 |
1 |
|
|
12 |
16.6 |
± 1.1 |
|
16 |
30.0 |
± 0.4 |
|
24 |
44.0 |
± 1.7 |
|
39 |
55.0 |
± 2.8 |
The longer of the two adjoining curves of Fig. 6 illustrates the regular course of these numbers with approximate accuracy
for such a small number of tests. As Fig. 6 shows, in the cases examined, the number of repetitions necessary for the memorisation
of series in which the number of syllables progressively increased, itself increases with extraordinary rapidity with the
increase in number of the syllables. 
At first the ascent of the curve is very steep, but later on it appears to gradually flatten out. For the mastery of five
times the number of syllables that can be reproduced after but one reading -- i.e., after about 3 seconds over 50 repetitions
were necessary, requiring an uninterrupted and concentrated effort for fifteen minutes.
The curve has its natural starting point in the zero point of the co-ordinates. The short initial stretch up to the point,
x=7, y=1, can be explained thus: in order to recite by heart series of 6, 5, 4, etc., syllables one reading, of course, is
all that is necessary. In my ease this reading does not require as much attention as does the 7-syllable one, but can become
more and more superficial as the number of syllables decreases.
Section 20. Tests Belonging to the Earlier Period
It goes without saying that since the results reported were obtained from only one person they have meaning only as related
to him. The question arises whether they are for this individual of a general significance -- i.e., whether, by repetition
of the tests at another time, they could be expected to show approximately the same amount and grouping.
A series of results from the earlier period furnishes the desired possibility of a control in this direction. They, again,
have been obtained incidentally (consequently uninfluenced by expectations and suppositions) and from tests made under different
conditions than those mentioned. These earlier tests occurred at an earlier hour of the day and the learning was continued
until the separate series could be recited twice in succession without mistake. A test comprised
|
|
15 |
series |
of |
10 |
syllables |
each, |
|
or |
8 |
" |
" |
13 |
" |
" |
|
or |
6 |
" |
" |
16 |
" |
" |
|
or |
4 |
" |
" |
19 |
" |
" |
So, again, four different lengths of series have been taken into account, but their separate values lie much closer together.
Since the repetitions -- which are in question here -- were not counted at all in the earlier period, their number had
to be calculated from the times. For this purpose the table on p. 31 has been used after corresponding interpolation. If the
numbers found are immediately reduced to one series each, and if along with it the two repetitions representing the recitation
are subtracted as above, we obtain:

The smaller curve of Fig. 6 exhibits graphically the arrangement of these numbers. As may be seen, the number of repetitions
necessary for learning equally long series was a little larger in the earlier period than in the later one. Because of its
uniformity this relation is to be attributed to differences in the experimental conditions, to inaccuracies in the calculations,
and perhaps also to the increased training of the later period. The older numbers fall very close to the position of the later
ones, and -- what is of chief importance -- the two curves lie as closely together throughout the short extent of their common
course as could be desired for tests separated by 3 1/2 years and unaffected by any presuppositions. There is a high degree
of probability, then, in favor of the supposition that the relations of dependence presented in those curves, since they remained
constant over a long interval of time, are to be considered as characteristic for the person concerned, although they are,
to be sure, only individual.
Section 21. Increase in Rapidity of Learning in the Case of Meaningful Material
In order to keep in mind the similarities and differences between sense and nonsense material, I occasionally made tests
with the English original of Byron's "Don Juan." These results do not properly belong here since I did not vary the length
of the amount to be learned each time but memorised on each occasion only separate stanzas. Nevertheless, it is interesting
to mention the number of repetitions necessary because of their contrast with the numerical results just given.
There are only seven tests (1884) to be considered, each of which comprised six stanzas. When the latter, each by itself,
were learned to the point of the first possible reproduction, an average of 52 repetitions (P.E.m = ±
0.6) was necessary for all six taken together. Thus, each stanza required hardly nine repetitions; or, if the errorless reproduction
is abstracted, scarcely eight repetitions.[2]
If it is born in mind that each stanza contains 80 syllables (each syllable, however, consisting on the average of less
than three letters) and if the number of repetitions here found is compared with the results presented above, there is obtained
an approximate numerical expression for the extraordinary advantage which the combined ties of meaning, rhythm, rhyme, and
a common language give to material to be memorised. If the above curve is projected in imagination still further along its
present course, then it must be supposed that I would have required 70 to 80 repetitions for the memorisation of a series
of 80 to 90 nonsense syllables. When the syllables were objectively and subjectively united by the ties just mentioned this
requirement was in my case reduced to about one-tenth of that amount.
Footnotes
[1] The objection might be made that, by means of this division, recourse made directly to the averages for the memorising
of the single series, and that in this way the result of the Fourth Chapter is disregarded. For, according to that, the averages
of the numbers obtained from groups of series could indeed be used for investigation into relations of dependence, but the
averages obtained from separate series could not be so used. I do not claim, however, that the above numbers, thus obtained
by division, form the correct average for the numbers belonging to the separate series, i.e., that the latter group
themselves according to the law of errors. But the numbers are to be considered as averages for groups of series, and, for
the sake of a better comparison with others -- a condition which in the nature of the case could not be everywhere the same
-- is made the same by division. The probable error, the measure of their accuracy, has not been calculated from the numbers
for the separate series but from those for the groups of series.
[2] For the sake of correct evaluation of the numbers and correct connection with possible individual observations
please note p. 24, 1. In order to procure uniformity of method the stanzas were always read through from beginning to end;
more difficult passages were not learned separately and then inserted. If that had been done, the times would have been much
shorter and nothing could have been said about the number of repetitions. Of course the reading was done at a uniform rate
of speed as far as possible, but not in the slow and mechanically regulated time that was employed for the series of syllables.
The regulation of speed was left to free estimation. A single reading of one stanza required 20 to 23 seconds.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER VI
RETENTION AS A FUNCTION OF THE NUMBER OF REPETITIONS
Section 22. Statement of the Problem
The result of the fourth chapter was as follows: When in repeated cases I memorised series of syllables of a certain length
to the point of their first possible reproduction, the times (or number of repetitions) necessary differed greatly from each
other, but the mean values derived from them had the character of genuine constants of natural science. Ordinarily, therefore,
I learned by heart homogeneous series under similar conditions with, on the average, a similar number of repetitions. The
large deviations of the separate values from each other change the total result not at all; but it would require too much
time to ascertain with exactness the number necessary for greater precision in detail.
What will happen, it may be asked, if the number of repetitions actually given to a certain series is less than is required
for memorisation or if the number exceeds the necessary minimum?
The general nature of what happens has already been described. Naturally the surplus repetitions of the latter alternative
do not go to waste. Even though the immediate effect, the smooth and errorless reproduction, is not affected by them, yet
they are not without significance in that they serve to make other such reproductions possible at a more or less distant time.
The longer a person studies, the longer he retains. And, even in the first ease, something evidently occurs even if the repetitions
do not suffice for a free reproduction. By them a way is at least opened for the first errorless reproduction, and the disconnected,
hesitating, and faulty reproductions keep approximating more and more to it.
These relations can be described figuratively by speaking of the series as being more or less deeply engraved in some mental
substratum. To carry out this figure: as the number of repetitions increases, the series are engraved more and more deeply
and indelibly; if the number of repetitions is small, the inscription is but surface deep and only fleeting glimpses of the
tracery can be caught; with a somewhat greater number the inscription can, for a time at least, be read at will; as the number
of repetitions is still further increased, the deeply cut picture of the series fades out only after ever longer intervals.
What is to be said in case a person is not satisfied with this general statement of a relation of dependence between the
number of repetitions and the depth of the mental impression obtained, and if he demands that it be defined more clearly and
in detail? The thermometer rises with increasing temperature, the magnetic needle is displaced to an increasing angle as the
intensity of the electric current around it increases. But while the mercury always rises by equal spaces for each equal increase
in temperature, the increase of the angle showing the displacement of the magnetic needle becomes less with a like increase
in the electric current. Which analogy is it which holds for the effect of the number of repetitions of the series to be memorised
upon the depth of the resulting impression? Without further discussion shall we make it proportional to the number of repetitions,
and accordingly say that it is twice or three times as great when homogenous series are repeated with the same degree of attention
twice or thrice as many times as are others? Or does it increase less and less with each and every constant increase in the
number of repetitions? Or what does happen?
Evidently this question is a good one; its answer would be of theoretical as well as practical interest and importance.
But with the resources hitherto at hand it could not be answered, nor even investigated. Even its meaning will not be quite
clear so long as the words "inner stability" and "depth of impression" denote something indefinite and figurative rather than
something clear and objectively defined.
Applying the principles developed in section 5, I define the inner stability of a series of ideas -- the degree of its
retainability -- by greater or less readiness with which it is reproduced at some definite time subsequent to its first memorisation.
This readiness I measure by the amount of work saved in the relearning of any series as compared with the wok necessary for
memorising a similar but entirely new series.
The interval of time between the two processes of memorisation is of course a matter of choice. I chose 24 hours.
Since in the case of this definition we are not trying to settle a matter of general linguistic usage, it cannot be properly
asked whether it is correct, but only whether it serves the purpose, or, at the most, whether it is applicable to the indefinite
ideas connected with the notion of different depths of mental impression. The latter will probably be granted But nothing
can be said in advance as to how well it fulfills its purpose. That can be judged only after more extensive results have been
obtained. And the character of the judgment will depend to a great extent on whether the results obtained with the help of
this means of measurement fulfill the primary demand which we make with reference to any system of measurement. It consists
in this, -- that if any change whatever is made in the controllable conditions of that scale, the results obtained by the
scale in its new form can be reduced to those of the old form by multiplication by some one constant. In our present case,
for example, it would consequently be necessary to know whether the character of the results would remain the same
if any other interval had been employed instead of that of 24 hours, arbitrarily chosen for measuring the after-effect of
repetitions, or whether as a consequence the entire rationale of the results would be different, just as the absolute values
are necessarily different. Naturally, this question cannot be decided a priori.
For ascertaining the relation of dependence between the increase in the number of repetitions of a series and the ever
deeper impression of it which result, I have formulated the problem as follows: If homogeneous series are impressed to different
extents as a result of different numbers of repetitions, and then 24 hours later are learned to the point of the first possible
reproduction by heart, how are the resulting savings in work related to each other and to the corresponding number of former
repetitions?
Section 23. The Tests and their Results
In order to answer the question just formulated, I have carried out 70 double tests, each of six series of 16 syllables
each. Each double test consisted in this, that the separate series -- each for itself -- were first read attentively a given
number of times (after frequently repeated readings they were recited by heart instead of read), and that 24 hours later I
relearned up to the point of first possible reproduction the series thus impressed and then in part forgotten. The first reading
was repeated 8, 16, 24, 32, 42, 53, or 64 times.
An increase of the readings used for the first learning beyond 64 repetitions proved impracticable, at least for six series
of this length. For with this number each test requires about 3/4 of an hour, and toward the end of this time exhaustion,
headache, and other symptoms were often felt which would have complicated the complicated of the test if the number of repetitions
had been increased.
The tests were equally divided among the seven numbers of repetitions investigated so that to each of them were allotted
10 double tests. The results were as follows for the six series of a single test taken together and without subtraction of
the time used for reciting.
After a preceding study of the series by means of "x" repetitions, they were learned 24 hours later with an expenditure
of "y" seconds.
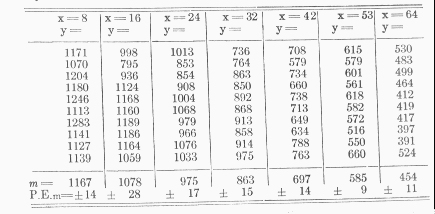
The preceding table of numbers gives the times actually used in learning by heart the series studied 24 hours previously.
Since we are interested not so much in the times used as the times saved we must know how long it would have taken to learn
by heart the same series if no previous study had been made. In the case of the series which were repeated 42, 53, and 64
times, this time can be learned from the tests themselves. For, in their case, the number of repetitions is greater than the
average minimum for the first possible reproduction, which in the case of the 16-syllable series (p. 46 [beginning of Ch.
5]) amounted to 31 repetitions. In their case, therefore, the point can be determined at which the first errorless reproduction
of that series appeared as the number of repetitions kept on increasing. But on account of the continued increase in the number
of repetitions and the resulting extension of the time of the test, the conditions were somewhat different from those in the
customary learning of series not hitherto studied. In the case of the series to which a smaller number of repetitions than
the above were given, the numbers necessary for comparison cannot be derived from their own records, since, as a part of the
plan of the experiment, they were not completely learned by heart. I have consequently preferred each time to find the saving
of work in question by comparison with the time required for learning by heart not the same but a similar series up to that
time unknown. For this I possess a fairly correct numerical value from the time of the tests in question: any six 16-syllable
series was learned, as an average of 53 tests, in 1,270 seconds, with the small probable error ±
7.
If all the mean values are brought together in relation to this last value, the following table results:

The simple relation approximately realised in these numbers is evident: the number of repetitions used to impress the series
(Column I) and the saving in work in 1arning the series 24 hours later as a result of such impression (Col. III) increase
in the same fashion. Division of the amount of work saved by the corresponding number of repetitions gives as a quotient a
practically constant value (Col. IV).
Consequently the results of the test may be summarised and formulated as follows: When nonsense series of 16 syllables
each were impressed in memory to greater and greater degrees by means of attentive repetitions, the inner depth of impression
in part resulting from the number of the repetitions increased, within certain limits, approximately proportionally to that
number. This increase in depth was measured by the greater readiness with which these series were brought to the point of
reproduction after 24 hours. The limits within which this relation was determined were on the one side, zero, and, on the
other, about double the number of repetitions that on the average just sufficed for learning the series.
For six series taken together the after-effect of each repetition -- i.e., the saving it brought about -- amounted
on the average to 12.7 seconds, consequently to 2.1 seconds for each single series. As the repetition of a series of 16 syllables
in itself takes from 6.6 to 6.8 seconds, its after-effect 24 hours later amounts to a scant third of its own duration. In
other words: for each three additional repetitions which I spent on a given day on the study of a series, I saved, in learning
that series 24 hours later, on the average, approximately one repetition; and, within the limits stated, it did not matter
how many repetitions altogether were spent on the memorisation of a series.
Whether the results found can claim any more general importance, or whether they hold good only for the single time of
their actual occurrence, and even then give a false impression of a regularity not otherwise present, I cannot now decide.
I have no direct control tests. Later, however, (chapter VIII, sec. 34) where results obtained in reference to quite a different
problem agree with the present results, I can bring forward indirect evidence on this point. I am therefore inclined to ascribe
general validity to these results, at least for my own case.
NOTE.--There is in the tests an inner inequality which I can neither avoid, nor remove by correction, but can only point
out. It is that a small number of repetitions of the series requires only a few minutes, and consequently come at a time of
unusual mental vitality. With 64 repetitions the whole work takes about 3/4 of an hour; the great part of the series is, therefore,
studied in a condition of diminished vigor or even of a certain exhaustion, and the repetitions will, consequently, be less
effective. It is just the reverse of this in the reproduction of the series the next day. The series impressed by 8 perusals
require three times as much time in order to be memorised as those perused 64 times. Consequently the latter will be learned
a little more quickly not only on account of their greater fixedness, but also because they are now studied for the most part
under better conditions. These irregularities are mutually opposed, as is evident, and therefore partially compensate each
other: the series prepared under comparatively unfavorable conditions are memorised under comparatively more favorable conditions,
and vice versa. I cannot tell, however, how far this compensation goes and how far any remaining inequality of conditions
disturbs the results.
Section 24. The Influence of Recollection
One factor in the regular course of the results obtained seems to deserve special attention. In ordinary life it is of
the greatest importance, as far as the form which memory assumes is concerned, whether the reproductions occur with accompanying
recollection or not, -- i.e., whether the recurring ideas simply return or whether a knowledge of their former existence
and circumstances comes back with them. For, in this second case, they obtain a higher and special value for our practical
aims and for the manifestations of higher mental life. The question now is, what connection is there between the inner life
of these ideas and the complicated phenomena of recollection which sometimes do and sometimes do not accompany the appearance
in consciousness of images? Our results contribute somewhat toward the answer to this question.
When the series were repeated 8 or 16 times they had become unfamiliar to me by the next day. Of course, indirectly, I
knew quite well that they must be the same as the ones studied the day before, but I knew this only indirectly. I did not
get it from the series, I did not recognise them. But with 53 or 64 repetitions I soon, if not immediately, treated them as
old acquaintances, I remembered them distinctly. Nothing corresponding to this difference is evident in the times for memorisation
and for savings of work respectively. They are not smaller relatively when there is no possibility of recollection
nor larger relatively when recollection is sure and vivid The regularity of the after-effect of many repetitions does
not noticeably deviate from the line that is, so to speak, marked out by a smaller number of repetitions although the
occurrence of this after-effect is accompanied by recollection in the first case just as indubitably as it lacks recollection
in the second case.
I restrict myself to pointing out this noteworthy fact. General conclusions from it would lack foundation as long as the
common cause cannot be proved.
Section 25. The Effect of a Decided Increase in the Number of Repetitions
It would be of interest to know whether the approximate proportionality between the number of repetitions of a series and
the saving of the work in relearning the latter made possible thereby, which in my own case seemed to take place within certain
limits, continues to exist beyond those limits. If, furthermore, as a result of each repetition a scant third of its own value
is saved up to be applied on the reproduction 24 hours later, I should be able to just reproduce spontaneously after 24 hours
a series of 16 syllables, the initial syllable being given, provided I had repeated it the first day thrice as many times
as were absolutely necessary for its first reproduction. As this requirement is 31-32 repetitions the attainment of the aim
in question would necessitate about 100 repetitions. On the supposition of the general validity of the relation found, the
number of repetitions to he made at a given time, in order that errorless reproduction might take place 24 hours later, could
be calculated for any kind of series for which, so to say, the "after-effect coefficient" of the repetitions had been ascertained.
I have not investigated this question by further increasing the number of repetitions of unfamiliar 16 syllable series
because, as has been already noted, with any great extension of the tests the increasing fatigue and a certain drowsiness
cause complications. However, I have made some trial tests partly with shorter series, and partly with fsmiliar series, all
of which confirmed the result that the proportion in question gradually ceases to hold with a further increase of repetitions.
Measured by the saving of work after 24 hours the effect of the later repetitions gradually decreases.
Series of 12 syllables (six of the series were each time combined into a test) were studied to the point of first possible
reproduction; and immediately after the errorless reproduction each series was repeated three times (in all four times) as
often as the memorisation (exclusive of the recital) had required. After 24 hours the same series were relearned to the first
possible reproduction. Four tests furnished the following results (the numbers indicate the repetitions):
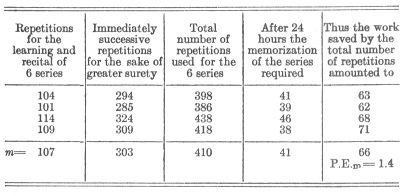
In my own case -- within reasonable limits -- the after-effect of the repetitions of series of 12 syllables after 24 hours
is a little smaller than is the case with 16 syllables; it must be estimated as at least three tenths of the sum total of
the repetitions. If this relation were approximately to continue to hold with very numerous repetitions, it would be reasonable
to expect that, after 24 hours, series on whose impression four times as many repetitions had been expended as were necessary
for their first reproduction could be recited without any further expenditure of energy. Instead of this, in the cases examined,
the relearning required about 35 per cent of the work required for the first recital. The effect of an average number of 410
repetitions was a saving of only one sixth of this sum. If now the first repetitions were represented by about three tenths
of their amount, the effect of the later repetitions must have been very slight.
Investigation of the following kind, which I do not here give in detail, led to the same result. Syllable series of different
lengths were gradually memorised by frequent repetitions which, however, did not all take place on one day, but were distributed
over several successive days (Chap. VIII). When, after several days, only a few repetitions were necessary in order to learn
the series by heart, they were repeated three or four times as often as was necessary, at this phase of memorisation, for
the first errorless reproduction. But in no single case did I succeed in an errorless reproduction of the series after 24
hours unless I had read them again once or several times. The influence of the frequent repetitions still appeared, indeed,
in a certain saving of work, but this became less in proportion to the decreasing amount of work to be saved. It was very
hard, by means of repetitions which had taken place 24 hours previously, to eliminate the last remnant of the work of relearning
a given series.
To summarise: The effect of increasing the number of repetitions of series of syllables on their inner fixedness in the
above defined sense grew at first approximately in proportion to the number of repetitions, then that effect decreased gradually,
and finally became very slight when the series were so deeply impressed that they could be repeated after 24 hours, almost
spontaneously. Since this decrease must be considered, gradual and continuous, its beginning would, in more accurate investigations,
probably have become evident even within the limits within which we found a proportionality, whereas no it is hidden on account
of its small amount and the wide limits of error.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER VII
RETENTTON AND OBLIVISCENCE AS A FUNCTION OF THE TIME
Section 26. Exp1anations of Retention and Obliviscence
All sorts of ideas, if left to themselves, are gradually forgotten. This fact is generally known. Groups or series of ideas
which at first we could easily recollect or which recurred frequently of their own accord and in lively colors, gradually
return more rarely and in paler colors, and can be reproduced by voluntary effort only with difficulty and in part. After
a longer period even this fails, except, to be sure, in rare instances. Names, faces, bits of knowledge and experience that
had seemed lost for years suddenly appear before the mind, especially in dreams, with every detail present and in great vividness;
and it is hard to see whence they came and how they managed to keep hidden so well in the meantime. Psychologists -- each
in accordance with his general standpoint -- interpret these facts from different points of view, which do not exclude each
other entirely but still do not quite harmonise. One set, it seems, lays most importance on the remarkable recurrence of vivid
images even after long periods. They suppose that of the perceptions caused by external impressions there remain pale images,
"traces," which, although in every respect weaker and more flighty than the original perceptions, continue to exist unchanged
in the intensity possessed at present. These mental images can not compete with the much more intense and compact perceptions
of real life; but where the latter are missing entirely or partly, the former domineer all the more unrestrainedly. It is
also true that the earlier images are more and more overlaid, so to speak, and covered by the later ones. Therefore, in the
case of the earlier images, the possibility of recurrence offers itself more rarely and with greater difficulty. But if, by
an accidental and favorable grouping of circumstances, the accumulated layers are pushed to one side, then, of course, that
which was hidden beneath must alppear, after whatever lapse of time, in its original and still existent vividness.[1]
For others[2] the ideas, the persisting images, suffer changes more and more affect their nature; the concept of obscuration comes in
here. Older ideas are repressed and forced to sink down, so to speak, by the more recent ones. As time passes one of these
general qualities, inner clearness and intensity of consciousness, suffers damage. Connections of ideas and series of ideas
are subject to the same process of progressive weakening; it is furthered by a resolution of the ideas into their components,
as a result of which the now but loosely connected members are eventually united in new combinations. The complete disappearance
of the more and more repressed ideas occurs only after a long time. But one should not imagine the repressed ideas in their
time of obscuration to be pale images, but rather to be tendencies, "dispositions," to recreate the image contents forced
to sink down. If these dispositions are somehow supported and strengthened, it may happen at any one moment that the repressing
and hindering ideas become depressed themselves, and that the apparently forgotten idea arises again in perfect clearness.
A third view holds that, at least in the case of complex ideas, obliviscence consists in the crumbling into parts and the
loss of separate components instead of in general obscuration. The idea of resolution into component parts recently spoken
of supplies here the only explanation. "The image of a complex object is dim in our memory not because as a whole with all
its parts present and in order it is illuminated by a feebler light of consciousness, but it is because it has become incomplete.
Some parts of it are entirely lacking. Above all the precise connection of those still extant is, in general, missing and
is supplied only by the thought that some sort of union once existed between them; the largeness of the sphere in which, without
being able to make a final decision, we think this or that connection equally probable, determines the degree of dimness which
we are to ascribe to the idea in question."[3]
Each of these opinions receives a certain, but not exclusive, support from the actual inner experiences, or experiences
supposed to be actual, which we at times have. And what is the reason? It is that these fortuitous and easily obtained inner
experiences are much too vague, superficial and capable of various interpretations to admit in their entirety of only a single
interpretation, or even to let it appear as of preponderating probability. Who could, with even tolerable exactness, describe
in its gradual course the supposed overlaying or sinking or crumbling of ideas? Who can say anything satisfactory about the
inhibitions caused by series of ideas of different extent, or about the disintegration that a firm complex of any kind suffers
by the use of its components in new connections? Everybody has his private "explanation" of these processes, but the actual
conditions which are to be explained are, after all, equally unknown to all of us.
If one considers the limitation to direct, unaided observation and to the chance occurrence of useful experiences, there
seems but little prospect of improvement in conditions. How will one for example determine the degree of obscuration reached
at a certain point, or the number of fragments remaining? Or how can the probable course of inner processes be traced if the
almost entirely forgotten ideas return no more to consciousness?
Section 27. Methods of Investigation of Actual Conditions
By the help of our method we have a possibility of indirectly approaching the problem just stated in a small and definitely
limited sphere, and, by means of keeping aloof for a while from any theory, perhaps of constructing one.
After a definite time, the hidden but yet existent dispositions laid down by the learning of a syllable-series may be strengthened
by a further memorisation of the series, and thereby the remaining fragments may be united again to a whole. The work necessary
for this compared with that necessary when such dispositions and fragments are absent gives a measure for what has been lost
as well as for what remains. The inhibitions which idea-groups of different sorts or extents may occasion in relation to others
must, as a result of the interposition of well defined complexes of ideas between learning and relearning, betray itself in
the more or less increased work of relearning. The loosening of a bond of connection by some other use of its components can
be investigated in a similar manner as follows: after a certain series has been studied, new combinations of the same series
are memorised and the change in the amount of work necessary for relearning the original combination is then ascertained.
First, I investigated the first mentioned of these relations and put the question: If syllable series of a definite kind
are learned by heart and then left to themselves, how will the process of forgetting go on when left merely to the influence
of time or the daily events of life which fill it? The determination of the losses suffered was made in the way described:
after certain intervals of time, the series memorised were relearned, and the times necessary in both cases were compared.
The investigations in question fell in the year 1879-80 and comprised 163 double tests. Each double test consisted in learning
eight series of 13 syllables each (with the exception of 38 double tests taken from 11-12 A.M. which contained only six series
each) and then in relearning them after a definite time. The learning was continued until two errorless recitations of the
series in question were possible. The relearning was carried to the same point; it occurred at one of the following times,
-- namely, after about one third of an hour, after 1 hour, after 9 hours, one day, two days, six days, or 31 days.
The times were measured from the completion of the first set of first learnings, as a consequence of which no great accuracy
was required in case of the longer intervals. The influence of the last four intervals was tested at three different times
of day (p.33 [end of Chapter III]). Some preliminary remarks are necessary before the results obtained can be communicated.
Similar experimental conditions may be taken for granted in the case of the series relearned after a number of whole days.
At any rate there is no way of meeting the actual fluctuations even when external conditions are as far as possible similar,
other than by a multiplication of the tests. Where the inner dissimilarity was presumably the greatest, namely after the interval
of an entire month, I approximately doubled the number of tests.
In the case of an interval of nine hours and an interval of one hour between learning and relearning, there existed, however,
a noticeably constant difference in the experimental conditions. In the later hours of the day mental vigor and receptivity
are less. The series learned in the morning and then relearned at a later hour, aside from other influences, require more
work for relearning than they would if the relearning were done at a time of mental vigor equal to that of the original learning.
Therefore, in order to become comparable, the numerical values found for relearning must suffer a diminution which, at least
in the case of the 8 hour interval, is so considerable that it cannot be neglected. It must be ascertained how much longer
it takes to learn at the time of day, B, series which were learned in a seconds at the time of day, A. The actual determination
of this quantity presupposes more tests than I, up to the present, possess. If a necessary but inexact correction is applied
to the numbers found for 1 and for 8 hours, these become even more unreliable than if left to themselves.
In the ease of the smallest interval, one third of an hour, the same drawback reappears, though to a less degree; but it
is probably compensated for by another circumstance. The interval as a whole is so short that the relearning of the first
series of a test followed almost immediately or after an interval of one or two minutes upon the learning of the last series
of the same test. For this reason the whole formed so to speak, one continuous test in which the relearning of the series
took place under increasingly unfavorable conditions as regards mental freshness. But on the other hand the relearning after
such a short interval was done rather quickly. It took hardly half of the time required for the learning. By this means the
interval between the learning and relearning of a certain series became gradually smaller. The later series therefore had
more favorable conditions with regard to the time interval. In view of the difficulty of more accurate determinations, I have
taken it for granted that these two supposed counteracting influences approximately compensated each other.
Section 28. Results
In the following table I denote by:
L the time of first learning of the series in seconds, just as they were found, therefore including the time for the two
recitations.
WL the time for relearning the series also including the recitations.
WLk the time of relearning reduced where necessary by a correction.
D the difference L-WL or L-WLk, as the case may be -- that is, the saving of work in the case of relearning.
Q the relation of this saving of work to the time necessary for the first learning, given as a per cent. In the calculation
of this quotient I considered only the actual learning time, the time for recitation having been subtracted.[4]
The latter was estimated as being 85 seconds for two recitations of 8 series of 13 syllables each; that would correspond
to a duration of 0.41 seconds for each syllable (p. 31 [Chapter III, Section 15]).
Thus Q= (100D )/(L-85)
Finally A, B, C mean the previously mentioned times of day, 10-11A.M., 11-12 A. M., 6-8 P. M.
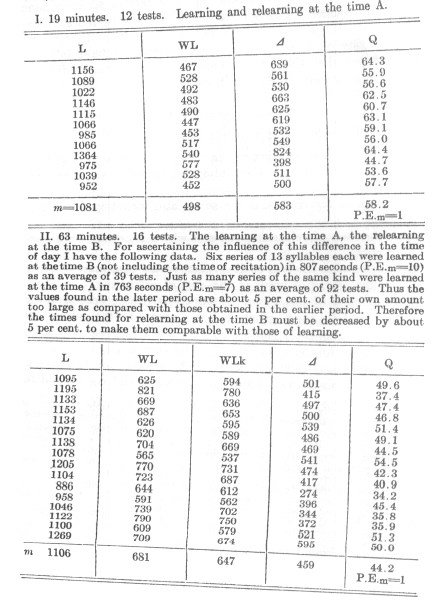
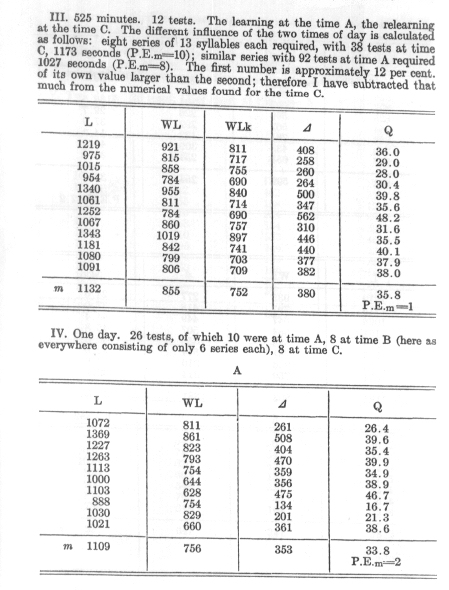
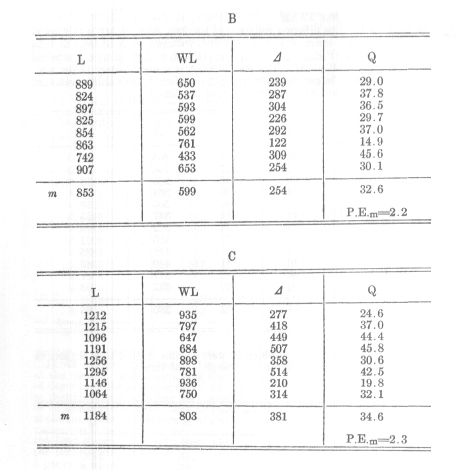

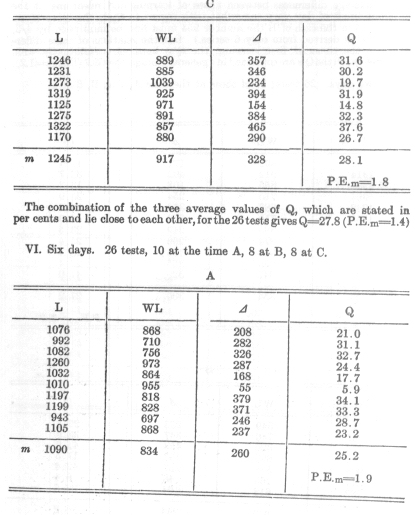
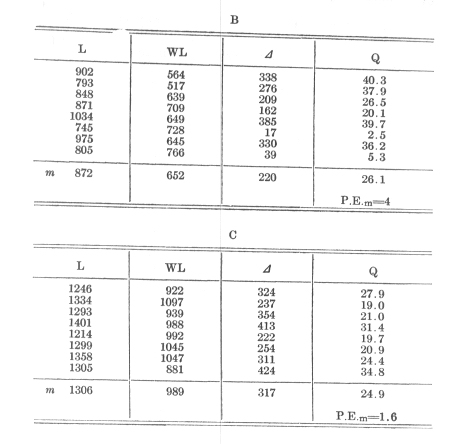

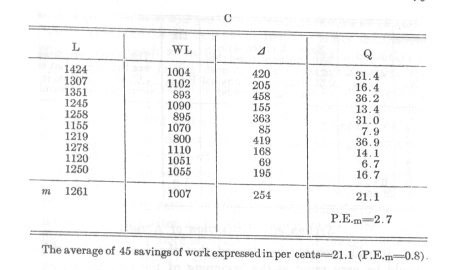
A hasty glance at the figures above reveals the fact that for each interval of time the savings in work which become evident
when the series is relearned have very fluctuating values. (This saving in work is each time the measure for the amount remembered
at the end of the interval.) This is especially the case with their absolute values (D ), but is
also the case with the relative values (Q). The results are taken from the earlier period and suffer from several disturbing
influences to which my attention was first drawn by the tests themselves.
In spite of all irregularities in detail, however, they group themselves as a whole with satisfactory certainty into an
harmonious picture. As a proof of this the absolute amount of the saving in work is of less value. The latter evidently depends
upon the time of day -- i.e., upon the changes in the time of the first learning dependent upon it. When this change
is greatest (time C), D also is greatest; for the time B, they are in 3/4 of the cases larger than
for the time A (after multiplying by 4/3). On the other hand, the values (Q) found for the relation of each saving of work
to the time originally spent, are apparently almost independent of this ratio. Their averages are close together for all three
times of day, and do not show any character of increase or decrease in the later hours. Accordingly I here tabulate the latter.
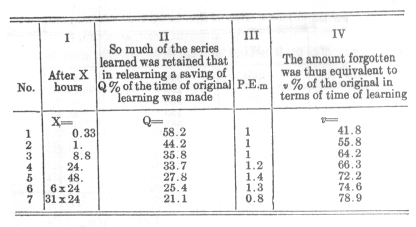
Section 29. Discussion of Results
1. It will probably be claimed that the fact that forgetting would be very rapid at the beginning of the process and very
slow at the end should have been foreseen. However, it would be just as reasonable to be surprised at this initial rapidity
and later slowness as they come to light here under the definite conditions of our experiment for a certain individual, and
for a series of 13 syllables. One hour after the end of the learning, the forgetting had already progressed so far that one
half the amount of the original work had to be expended before the series could be reproduced again; after 8 hours the work
to be made up amounted to two thirds of the first effort. Gradually, however, the process became slower so that even for rather
long periods the additional loss could be ascertained only with difficulty. After 24 hours about one third was always remembered;
after 6 days about one fourth, and after a whole month fully one fifth of the first work persisted in effect. The decrease
of this after-effect in the latter intervals of time is evidently so slow that it is easy to predict that a complete vanishing
of the effect of the first memorisation of these series would, if they had been left to themselves, have occurred only after
an indefinitely long period of time.
2. Least satisfactory in the results is the difference between the third and fourth values, especially when taken in connection
with the greater difference between the fourth and fifth numbers. In the period 9-24 hours the decrease of the after-effect
would accordingly have been 2 1/2 per cent. In the period 24 to 48 hours it would have been 6.1 per cent; in
the later 24 hours, then, about three times as much as in the earlier 15. Such a condition is not credible, since in the case
of all the other numbers the decrease in the after-effect is greatly retarded by an increase in time. It does not become credible
even under the plausible assumption that night and sleep, which form a greater part of the 15 hours but a smaller part of
the 24, retard considerably the decrease in the after-effect.
Therefore it must be assumed that one of these three values is greatly affected by accidental influences. It would fit
in well with the other observations to consider the number 33.7 per cent for the relearning after 24 hours as somewhat too
large and to suppose that with a more accurate repetition of the tests it would be 1 to 2 units smaller. However, it is upheld
by observations to be stated presently, so that I am in doubt about it.
3. Considering the special, individual, and uncertain character of our numerical results no one will desire at once to
know what "law" is revealed in them. However, it is noteworthy that all the seven values which cover intervals of one third
of an hour in length to 31 days in length (thus from singlefold to 2,000fold) may with tolerable approximation be put into
a rather simple mathematical formula. I call:
t the time in minutes counting from one minute before the en(l of the learning,
b the saving of work evident in relearning, the equivalent of the amount remembered from the first learning expressed
in percentage of the time necessary for this first learning,
c and k two constants to be defined presently
Then the following formula may be written:
b = 100k/((log t)c +k)
By using common logarithms and with merely approximate estimates, not involving exact calculation by the method of least
squares,
k = 1.84
c = 1.25
Then the results are as follows:
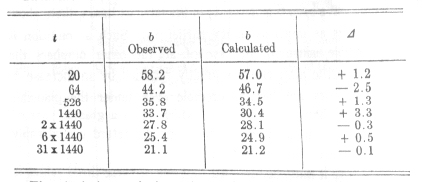
The deviations of the calculated values from the observed values surpass the probable limits of error only at the second
and fourth values. With regard to the latter I have already expressed the conjecture that the test might have given here too
large a value; the second suffers from an uncertainty concerning the correction made. By the determination made for t,
the formula has the advantage that it is valid for the moment in which the learning ceases and that it gives correctly b=100.
In the moment when the series can just be recited, the relearning, of course, requires no time, so that the saving is equal
to the work expended.
Solving the formula for k we have
k = b(log t)c/(100-b)
This expression, 100-b the complement of the work saved, is nothing other than the work required for relearning,
the equivalent of the amount forgotten from the first learning. Calling this, v, the following simple relation results:
b/v = k/(log t)c
To express it in words: when nonsense series of 13 syllables each were memorised and relearned after different intervals,
the quotients of the work saved and the work required were about inversely proportional to a small power of the logarithm
of those intervals of time. To express it more briefly and less accurately: the quotients of the amounts retained and the
amounts forgotten were inversely as the logarithms of the times.
Of course this statement and the formula upon which it rests have here no other value than that of a shorthand statement
of the above results which have been found but once and under the circumstances described. Whether they possess a more general
significance so that, under other circumstances or with other individuals, they might find expression in other constants I
cannot at the present time say.
Section 30. Control Tests
At any rate, even though only for my own case, I can to a certain extent give support to two of the values mentioned by
tests which were made at other periods.
From a period even further back than that of the investigations above mentioned I possess several tests with series of
ten syllables, fifteen series composing one test. The series were first memorised and then, at an average of 18 minutes after
the first learning, each series was relearned. Six tests had the following results:--
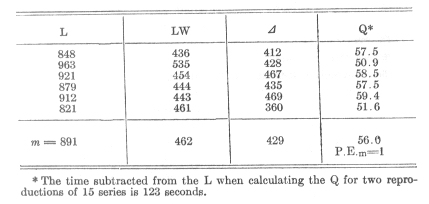
When relearning series of ten syllables each, 18 minutes after the first memorisation, 56 per cent of the work originally
expended was therefore saved. The number agrees satisfactorily with the one found above (p. 68 [section 28]) for the relearning
of series of syllables of 13 syllables each after 19 minutes, 58 per cent. Also the fact that the latter, notwithstanding
the longer interval, is still a little greater, harmonises completely, as will be seen, with the results of the next chapter.
According to them, shorter series, when memorised, are forgotten a little more quickly than longer once.
From the period of 1883-84, I have seven tests, consisting of nine series of 12 syllables each that were relearned 24 hours
after the first memorisation. The following results were obtained:
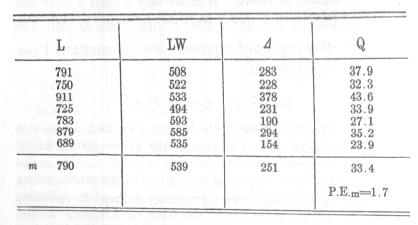
The after-effect of the first memorisation still noticeable after 24 hours, was here equivalent to a saving of work of
33.4 per cent of the first expenditure. This number also agrees satisfactorily with the one communicated above for the relearning
of series of 13 syllables each after 24 hours (33.7 per cent), although these two were obtained at far separated time-periods
and in the course of widely different investigations.
Footnotes
[1] This is the opinion of Aristotle and is still authoritative for many people. Lately, for instance, Delboeuf has taken
it up again, and has used it as a complement to his "théorie générale de la sensibilité." In his article, Le sommeil et
les rêves (Rev. Philos. IX, p. 153 f.), he says: Nous voyons maintenant que tout acte de sentiment, de pensée ou de volition
en vertu d'une loi universelle imprime en nous une trace plus ou moins profonde, mais indélébile, généralement gravée sur
une infinité de traits antérieurs, surchargée plus tard d'une autre infinité de linéaments de toute nature. mais dont l'écriture
est néanmoins indéfiniment susceptible de reparaître vive et nette au jour." (We see now that by a general law every act of
feeling, thought or will leaves a more or less deep but indelible impress upon our mind, that such a tracing is usually graven
upon an infinite number of previous traces and later is itself overlaid with innumerable others but nevertheless is still
capable of vivid and clear reappearance.) It is true that he proceeds: "néanmoins . . . il y a quelque vérité dans l'opinion
qui veut que la mémoire non seulement se fatigue mais s'oblitère" (nevertheless . . . there is some truth in the opinion that
memory not only becomes fatigued but that it disappears"), but he explains this by the theory that one memory might hinder
another from appearing. Si un souvenir ne chasse pas l'autre, on peut du moins prétendre qu'un souvenir empêche l'autre et
qu'ainsi pour la substance cérébrale, chez l'individu, il y a un maximum de saturation." (If one recollection does not actually
drive out another, it may at least be maintained that one recollection hinders the other and that thus the brain of each individual
is saturtated.)
The curious theory of Bain and others that each idea is lodged in a separate ganglion cell, an hypothesis impossible both
psychologically and physiologically, is also rooted to a certain extent in Aristotle's view.
[2] Herbart and his adherents. See, for instance, Waitz, Leehrbuch der Psychologie Sect. 16
[3] Lotze, Metaphysik (1879), p. 521; also Mikrokosoms (3) I, p. 231 ff.
[4] A theoretically correct determination of the Probable Errors of the differences and quotients found
would be very difficult and troublesome. The directly observed values L and WL would have to be made the basis of it. But
the ordinary rules of the theory of errors cannot he applied to these values, because these rules are valid only for observations
gained independently of one another, whereas L and WL are inwardly connected because they were obtained from the same series.
The source of error, "difficulty of the series," does not vary by chance, but in the same way for each pair of values. Therefore
I took here the learning and relearning of the series as a single test and the resulting D or Q,
as the case may be, as its numerical representative. From the independently calculated D and Q, the
probable errors were then calculated just as from directly observed values. That is sufficient for an approximate estimate
of the reliability of the numbers.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER VIII
RETENTION AS A FUNCTION OF REPEATED LEARNING
Section 31. Statement of the Problem and the Investigation
Series of syllables which have been learned by heart, forgotten, and learned anew must be similar as to their inner conditions
at the times when they can be recited. The energy of the ideational activity which is directed upon them and which serves
to establish them is in both cases so far heightened that quite similar combinations of movements occur in connection with
them. For the period after the recital this inner similarity ceases. The series are gradually forgotten, but -- as is sufficiently
well known -- the series which have been learned twice fade away much more slowly than those which have been learned but once.
If the re-learning is performed a second, a third or a greater number of times, the series are more deeply engraved and fade
out less easily and finally, as one would anticipate, they become possessions of the soul as constantly available as other
image-series which may be meaningful and useful.
I have attempted to obtain numerical data on the relation of dependence which exists between the permanence of retention
of a series and the number of times it has been brought, by means of renewed learning, to a just possible reproduction. The
relation is quite similar to that described in Chapter VI as existing between the surety of the series and the number of its
repetitions. In the present case, however, the repetitions do not take place all at once, but at separate times and in ever
decreasing frequency. On account of our limited insight into the inner connection of these processes we would not be justified
in venturing an assertion about one relation on the basis of the other.
Only one value of the time interval between the separate re-learnings was chosen, namely, 24 hours. Instead of changing
intervals, series of different lengths were chosen for the investigation, the lengths being 12, 24 and 36 syllables. A single
test consisted of nine series of the first length, or three of the second, or two of the third. In addition to this I carried
out several tests with six stanzas of Byron's "Don Juan."
The plan of the experiment was, then, as follows: The required number of series was first learned and then, at the same
hour on successive days, it was relearned to the point of first possible reproduction. In the case of the series of syllables,
the number of days was six; in the case of Byron's stanzas, it was only four. Thus, on the fifth day, the stanzas were correctly
repeated without any preliminary reproduction and the problem, accordingly, no longer existed. For each kind of series, seven
trials were employed. The total number of separate tests was, in con-sequence, 154, a number of which required only a few
minutes for their execution.
The entries of the following tables indicate the repetitions which were necessary in order to bring the series concerned
to the first possible reproduction (including this); the Roman figures designate the successive days.
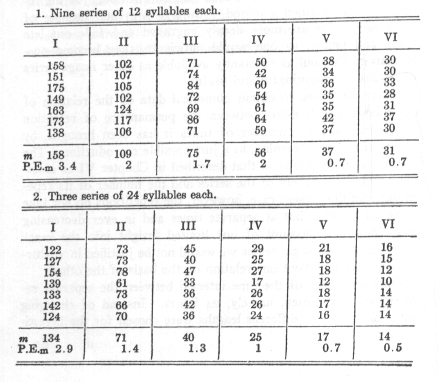
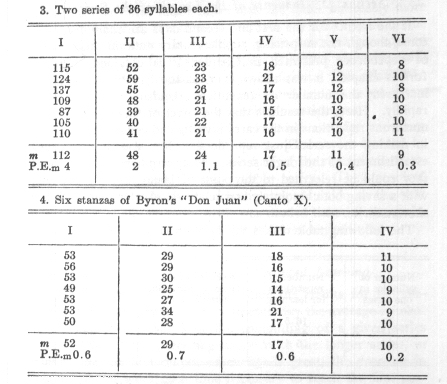
In order to bring out more dearly the separate relations which exist between the resulting averages, it is necessary to
reduce the total figures to the same unit -- i.e., to divide them in each case by the number of series constituting
a single trial. If this is done and the repetition necessary for the recital is deducted, the following table results, fractions
being given to the nearest half or quarter.

From several points of view these numbers require further consideration.
Section 32. Influence of the Length of the Series
If the results for the first and second days are examined, welcome, though not surprising, supplementary data on the relation
of dependence presented in Chapter V is obtained. In the former chapter, it was shown that, as the length of the series increased,
the number of repetitions requisite increased very rapidly. Here, the result is that the effect of this need of more numerous
repetitions in the cases investigated consists not merely in making the series just reproducible, but also in the firmer establishment
of the longer series. After an interval of 24 hours they could be relearned to the point of being just reproducible with a
saving both absolutely and relatively greater than with the shorter series.
The following table makes this relation clear.

The saving in the case of the shortest of the series investigated is one third for the second learning as compared with
the first; while with the longest series, it is six tenths. It can be said, therefore, that by being learned to the first
possible reproduction the series of 36 syllables is approximately twice as firmly established as the series of 12 syllables.
In this there is nothing new. On the basis of the familiar experience that that which is learned with difficulty is better
retained, it would have been safe to prophesy such an effect from the greater number of repetitions. That which probably would
not have been anticipated and which also demands attention, is the more definite determination of this general relation. So
far as the numbers go, they seem to show that, between the increase of the repetitions necessary for the first learning and
the inner stability of the series effected by them, there is no proportionality. Neither the absolute nor the relative saving
of work advances in the same way as the number of repetitions; the former advance much faster and the latter noticeably more
slowly. It cannot, therefore, be said in any exact sense of the words that the more frequently a series needs to be repeated
to-day in order to be learned by heart the more repetitions will be saved in its reproduction after 24 hours. The relation
in force seems to be much more complicated and its exact determination would require more extensive investigations.
The relation of repetitions for learning and for repeating English stanzas needs no amplification. These were learned by
heart on the first day with less than half of the repetitions necessary for the shortest of the syllable series. They acquired
thereby so great stability that for their reproduction on the next day proportionally no more work was needed than for the
semi of 24 syllables -- i.e., about half of the first expenditure.
Section 33 Influence of Repeated Learning
We will now take into consideration the results for the successive days taken as a whole. On each day the average number
of repetitions necessary for the committing of a given series is less than on the preceding day. With the longer series, in
whose case the first output of energy is great, the decrease in the amount of work each time necessary to reach the first
possible reproduction is proportionally rapid. With the shorter series, where the first output is small, the decrease is proportionally
slow. On this account the numbers of repetitions necessary for the different series approach each other more and more. With
the series of 24 and 36 syllables this is apparent even from the second day; from the fourth day on, the numbers fall absolutely
together. And by the fifth day they have approached very closely to the number of repetitions still necessary, in accordance
with the slower decrease, for the learning of the 12-syllable series.
A simple conformity to law cannot be discovered in this successively decreasing necessity for work. The quotients of the
necessary repetitions on two successive days approach unity. If the final repetition were not subtracted, as was done in the
concluding table of Section 31, but were reckoned in, this approach would be somewhat faster. (In the case of the English
stanzas it generally takes place only under these conditions.)
Nevertheless the course of the numbers cannot be described by a simple formula.
Rather is this the case if one takes into consideration, not the gradually decreasing necessity for work, but the just
as gradually decreasing saving of work.
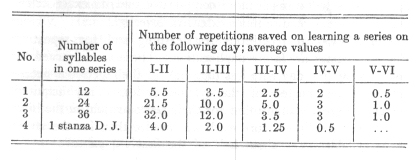
Of these numerical sequences two -- namely, the second and fourth rows -- form with great approximation a decreasing geometrical
progression with the exponent 0.5. Very slight changes in the numbers would be sufficient fully to bring out this conformity.
By slight changes, the first row might also be transformed into a geometrical progression with the exponent 0.6. On the contrary,
a large error in the results of investigation would need to be assumed in order to get out of Row 3 any such geometric progression
(whose exponent would then be about one third).
If not for all, yet for most, of the results found, the relation can be formulated as follows: If series of nonsense syllables
or verses of a poem are on several successive days each time learned by heart to the point of the first possible reproduction,
the successive differences in the repetitions necessary for this form approximately a decreasing geometrical progression.
In the case of syllable-series of different lengths, the exponents of these progressions were smaller for the longer series
and larger for the shorter ones.
Although the tests just described were individually not more protracted than the others, yet relatively they required many
days, and the average values were consequently derived from a rather small number of observations. So here, even more than
elsewhere, I am unable to affirm that the simple conformity to law approximately realised in the results so far obtained would
stand the test of repetition or wider extension of research. I content myself by calling attention to it without emphasis.
Section 34. Influence of the Separate Repetitions
The problem of the present chapter is, as has already been pointed out, closely related to that of Chapter VI. In both
cases the investigation concerns the influence of an increasing number of repetitions on the fixation of the series of syllables,
a fixation made increasingly stronger thereby. In the former case the total number of repetitions immediately succeeded each
other without regard to whether the spontaneous reproduction of the series was obtained through them or to how it was obtained.
In this case the repetitions were distributed over several days and tile attainment of the first possible reproduction was
employed for their apportionment on the separate days. If, now, the results obtained in both cases have, at least for my own
personality, any wider validity, we should expect that in so far as they are comparable, they would harmonise. That is, we
should expect in this case as in the former that the effect of the later repetitions (therefore, those of the 2nd, 3rd, and
later days), would at first be approximately as great as that of the earlier, and later would decrease more and more.
A more exact comparison is in the nature of the case not now possible. In the first place, the series of Chapter VI and
the present ones are of different length. In the second place, the detailed ascertainment of the effect of the repetitions
of the successive days taken solely by themselves would be possible only through assumptions which might be plausible enough
on the basis of the data presented, but which would be easily controvertible on account of the insecurity of these data.
We found, for example, that nine 12-syllable series were learned on six successive days by means of 158, 109, 75, 56, 37
and 31 repetitions. The effect of the first 158 repetitions is here immediately given in the 109 repetitions of the succeeding
day in the difference, 158-109. But if we wish to know the intrinsic effect of these 109 repetitions, namely the saving effected
by them, on the third day, we could not simply take the difference, 109-75. We should need to know, rather, with bow many
repetitions (x) the series would have been learned on the third day if no repetitions had occurred on the second, and
we should then have in the difference, x-75, the separate effect of the 109 repetitions actually given. Since the forgetting
increased somewhat from the second to the third day, x would be somewhat greater than 109. In the same way, for the
determination of the effect of the 75 repetitions of the third day, we should need to learn in some way or other with how
many repetitions (y), the series would have been learned by heart on the fourth day which, on the first day, required
158; and on the second, 109. The difference, y-56, would then give the measure of that effect; and so on. For the ascertainment
of x, the results of Chapter VII give a certain basis. There the result was that, in the case of 13-syllable series, the amount
forgotten at the end of 24 hours was to that forgotten at the end of 2x24 hours as 66 to 72. But the employment of this relation,
itself insecure, would be justifiable only in case of the 12-syllable series, and would accordingly not help in the determination
of y, etc. One could at the best suppose that the resulting quotients would approximate yet more closely to unity.
Accordingly I renounce these uncertain assumptions, and content myself with presenting the relations of the successive
repetitions to the successive savings by showing that the presupposed pure effect of the separate repetitions would be represented
by somewhat greater and presumably less divergent numbers.
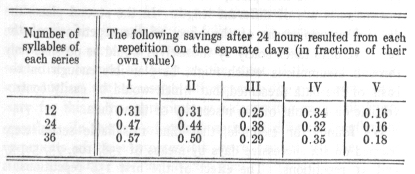
Although the course of these figures, which are, as has been said, inexact as to their absolute values, is tolerably regular
in the case of the 24-syllable series only, its general character agrees very well with what would be expected from the results
of Chapter IV. The effect of the repetitions is at first approximately constant, the saving in work which results from these
repetitions increases accordingly for a while proportional to their number. Gradually the effect becomes less; and finally,
when the series has become so firmly fixed that it can be repeated almost spontaneously after 24 hours, the effect is shown
to be decidedly less. The results of the fourth and the present chapter, as far as can be seen, Support each other.
Nevertheless, there is a noteworthy distinction to which I call attention. We found above (p.60 [end of Chapter VI]) that
six 12-syllable series, which had been learned at a given time with an average of 410 repetitions, could be learned
by heart at the end of 24 hours with, on the average, 41 repetitions. For a single 12-syllable series, accordingly, 68 immediately
successive repetitions had the effect of making possible an errorless recital on the following day after 7 repetitions. In
the present research with distribution of the repetitions over several days the same effect appears on the fourth day: 9 12-Syllable
Series were learned by heart with 56 repetitions. Each series, therefore, was learned with about 6 repetitions. But the number
of repetitions which were necessary for the production of this effect in the case of the nine series amounted to only 158+109+75=342.
For a single series, therefore, the number was 38. For the relearning of a 12-syllable series at a definite time, accordingly,
38 repetitions, distributed in a certain way over the three preceding days, had just as favorable an effect as 68 repetitions
made on the day just previous. Even if one makes very great concessions to the uncertainty of numbers based on so few researches,
the difference is large enough to be significant. It makes the assumption probable that with any considerable number of
repetitions a suitable distribution of them over a space of time is decidedly more advantageous than the massing of them
at a single time.
With this result, found here for only very limited conditions, the method naturally employed in practice agrees. The school-boy
doesn't force himself to learn his vocabularies and rules altogether at night, but knows that be must impress them again in
the morning. A teacher distributes his class lesson not indifferently over the period at his disposal, but reserves in advance
a part of it for one or more reviews.
Memory: A Contribution to Experimental Psychology
Hermann Ebbinghaus (1885)
Translated by Henry A. Ruger & Clara E. Bussenius (1913)
CHAPTER IX
RETENTION AS A FUNCTION OF THE ORDER OF
SUCCESSION OF THE MEMBERS OF THE SERIES
"How odd are the connections
Of human thoughts which jostle in their flight."
Section 35. Association according to Temporal Sequence and its Explanation
I shall now discuss a group of investigations made for the purpose of finding out the conditions of association. The results
of these investigations are, it seems to me, theoretically of especial interest.
The non-voluntary re-emergence of mental images out of the darkness of memory into the light of consciousness takes place,
as has already been mentioned, not at random and accidentally, but in certain regular forms in accordance with the so-called
laws of association. General knowledge concerning these laws is as old as psychology itself, but on the other hand a more
precise formulation of them has remained -- characteristically enough -- a matter of dispute up to the very present. Every
new presentation starts out with a reinterpretation of the contents of a few lines from Aristotle, and according to the condition
of our knowledge it is necessary so to do.
Of these "Laws," now -- if, in accordance with usage and it is to be hoped in anticipation of the future, the use of so
lofty a term is permitted in connection with formulae of so vague a character -- of these laws, I say, there is one which
has never been disputed or doubted. It is usually formulated as follows:
Ideas which have been developed simultaneously or in immediate succession in the same mind mutually reproduce each other,
and do this with greater ease in the direction of the original succession and with a certainty proportional to the frequency
with which they were together.
This form of non-voluntary reproduction is one of the best verified and most abundantly established facts in the whole
realm of mental events. It permeates inseparably every form of reproduction, even the so-called voluntary form. The function
of the conscious will, for example, in all the numerous reproductions of the syllable-series which we have come to know, is
limited to the general purpose of reproduction and to laying hold of the first member of the series. The remaining members
follow automatically, so to speak, and thereby fulfill the law that things which have occurred together in a given series
are reproduced in the same order.
However, the mere recognition of these evident facts has naturally not been satisfying and the attempt has been made to
penetrate into the inner mechanism of which they are the result. If for a moment we try to follow up this speculation concerning
the Why, before we have gone more than two steps we are lost in obscurities and bump up against the limits of
our knowledge of the How.
It is customary to appeal for the explanation of this form of association to the nature of the soul. Mental events, it
is said, are not passive happenings but the acts of a subject. What is more natural than that this unitary being should bind
together in a definite way the contents of his acts, themselves also unified? Whatever is experienced simultaneously or in
immediate succession is conceived in one act of consciousness and by that very means its elements are united and the unison
is naturally stronger in proportion to the number of times they are entwined by this bond of conscious unity. Whenever, now,
by any chance one part only of such a related complex is revived, what else can it do than to attract to itself the remaining
parts?
But this conception does not explain as much as it was intended to do. For the remaining parts of the complex are not merely
drawn forth but they respond to the pull in an altogether definite direction. If the partial contents are united simply by
the fact of their membership in a single conscious act and accordingly all in a similar fashion, how does it come about that
a sequence of partial contents returns in precisely the same order and not in any chance combination? In order to make this
intelligible, one can proceed in two ways.
In the first place it can be said that the connection of the things present simultaneously in a single conscious act is
made from each member to its immediate successor but not to members further distant. This connection is in some way inhibited
by the presence of intermediate members, but not by the interposition of pauses, provided that the beginning and end of the
pause can be grasped in one act of consciousness. Thereby return is made to the facts, but the advantage which the whole plausible
appeal to the unitary act of consciousness offered is silently abandoned. For, however much contention there may be over the
number of ideas which a single conscious act may comprehend, it is quite certain that, if not always, at least in most cases,
we include more than two members of a series in any one conscious act. If use is made of one feature of the explanation, the
characteristic of unity, as a welcome factor, the other side, the manifoldness of the members, must be reckoned with, and
the right of representation must not be denied it on assumed but unstatable grounds. Otherwise, we have only said, -- and
it is possible that we will have to be content with that -- that it is so because there are reasons for its being so.
There is, consequently, the temptation to use this second form of statement. The ideas which are conceived in one act of
consciousness are, it is true, all bound together, but not in the same way. The strength of the union is, rather, a decreasing
function of the time or of the number of intervening members. It is therefore smaller in proportion as the interval which
separates the individual members is greater. Let a, b, c, d be a series which has been presented in a single conscious
act, then the connection of a with b is stronger than that of a with the later c; and the latter
again is stronger than that with d. If a is in any way reproduced, it brings with it b and c and
d, but b, which is bound to it more closely, must arise more easily and quickly than c, which is closely
bound to b, etc. The series must therefore reappear in consciousness in its original form although all the members
of it are connected with each other.
Such a view as this has been logically worked out by Herbart. He sees the basis of the connection of immediately successive
ideas not directly in the unity of the conscious act, but in something similar: opposed ideas which are forced together in
a unitary mind can be connected only by partial mutual inhibition followed by fusion of what remains. Yet this, for our purpose,
is not essential. He proceeds as follows:
"Let a series, a, b, c, d . . . be given in perception, then a, from the very first moment
of the perception and during its continuance, is subjected to inhibition by other ideas present in consciousness. While a,
already partially withdrawn from full consciousness, is more and more inhibited, b comes up. The latter, at first uninhibited,
fuses with the retiring a. c follows and, itself uninhibited, is united with the fast dimming b and the
still more obscured a. In a similar fashion d follows and unites itself in varying degrees with a, b, and
c. Thus there originates for each of these ideas a law according to which, after the whole series has been forced out
of consciousness for some tune, in its own way on its renewed appearance each idea struggles to call up every other idea of
the same series. Suppose that a arises first, it is more closely connected with b, less with c, still
less with d, etc. But, taken in the reverse order b, c, and d, all in an uninhibited condition, are fused
with what remains of a. Consequently a seeks to bring them completely back to the form of an uninhibited idea;
but its effect is quickest and strongest upon b, slower on c and still slower on d, etc. (whereby closer
inspection shows that b sinks again while c is still rising, and that in the same way c sinks while d
rises, etc.). In short, the series runs off as it was originally given. If we suppose, on the contrary, that c was
the one initially reproduced, then its effect on d and the succeeding members is similar to that revealed by a --
i.e., the series c, d, . . . runs off gradually in conformity with its order. b and a, however, experience
an altogether different influence. With their separate conscious residues, the uninhibited c had fused; its effect
upon a and b was therefore without loss of power and without delay, but this effect was limited to bringing
back the conscious residues of a and b bound up with it, only a part of b and a still smaller part of
a being recalled to consciousness. This, then, is what happens if the process of recall begins anywhere at the middle
of a known series. That which preceded the point of recall rises at once in graded degrees of clearness. That which followed,
on the contrary, runs off in the order of the original series. The series, however, never runs backwards, an anagram is never
formed out of a well understood word without voluntary effort."[1]
According to this conception, therefore, the associative threads, which hold together a remembered series, are spun not
merely between each member and its immediate successor, but beyond intervening members to every member which stands to it
in any close temporal relation. The strength of the threads varies with the distance of the members, but even the weaker of
them must be considered as relatively of considerable significance.
The acceptance or rejection of this conception is clearly of great importance for our view of the inner connection of mental
events, of the richness and complexity of their groupings and organisation. But it is clearly quite idle to contend about
the matter if observation is limited to conscious mental life, to the registration of that which whirls around by chance on
the surface of the sea of life.
For, according to the hypothesis, the threads which connect one member to its immediate successor although not the only
one spun, are, however, stronger than the others. Consequently, they are, in general, as far as appearances in consciousness
are concerned, the important ones, and so the only ones to be observed.
On the other hand, the methods which lie at the basis of the researches already described permit the discovery of connections
of even less strength. This is done by artificially strengthening these connections until they reach a definite and uniform
level of reproducibility. I have, therefore, carried on according to this method a rather large number of researches to test
experimentally in the field of the syllable-series the question at issue, and to trace an eventual dependence of the strength
of the association upon the sequence of the members of the series appearing in succession in consciousness.
Section 36. Methods of Investigation of Actual Behavior
Researches were again carried out with six series of 16 syllables each. For greater clearness the series are designated
with Roman numbers and the separate syllables with Arabic. A syllable group of the following form constituted, then, each
time the material for research:
I(1) I(2) I(3) . . . . . . . . . . . . . . . . . . . I(15) I(16)
II(1) II(2) II(3) . . . . . . . . . . . . . . . . .
II(15) II(16)
.
.
.
VI(1) . . . . . . . . . . . . . . . . . . . . . . . . VI(15) VI(16)
If I learn such a group, each series by itself, so that it can be repeated without error, and 24 hours later repeat it
in the same sequence and to the same point of mastery, then the latter repetition is possible in about two thirds of the time
necessary for the first.[2] The resulting saving in work of one third clearly measures the strength of the association formed during the first learning
between one member and its immediate successor.
Let us suppose now that the series are not repeated in precisely the same order in which they were learned. The syllables
learned in the order I(1) I(2) I(3) . . . I(15) I(16) may for example be repeated in the order I(1) I(3) 1(5) . . . I(15)
I(2) I(4) I(6) . . . I(16), and the remaining series with a similar transformation. There will first be, accordingly,
a set composed of all the syllables originally in the odd places and then a set of those originally in the even places, the
second set immediately following the first. The new 16-syllable series, thus resulting, is then learned by heart. What will
happen? Every member of the transformed series was, in the original series, separated from its present immediate neighbor
by an intervening member with the exception of the middle term where there is a break. If these intervening members are actual
obstructions to the associative connection, then the transformed series are as good as entirely unknown. In spite of the former
learning of the series in the original sequence, no saving in work should be expected in the repetition of the transformed
series. If on the other hand in the first learning threads of association are spun not merely from each member to its immediate
successor but also over intervening members to more distant syllables, there would exist, already formed, certain predispositions
for the new series. The syllables now in succession have already been bound together secretly with threads of a certain strength.
In the learning of such a series it will be revealed that noticeably less work is required than for the learning of an altogether
new series. The work, however, will be greater than in relearning a given series in unchanged order. In this case, again,
the saving in work will constitute a measure of the strength of the associations existing between two members separated by
a third. If from the original arrangement of the syllables new series are formed by the omission of 2, 3, or more intervening
members, analogous considerations result. The derived series will either be learned without any noticeable saving of work,
or a certain saving of work will result, and this will be proportionally less as the number of intervening terms increases.
On the basis of these considerations I undertook the following experiment. I constructed six series of 16 syllables each
with the latter arranged by chance. Out of each group a new one was then constructed also composed of six series of 16 syllables
each. These new groups were so formed that their adjacent syllables had been separated in the original series by either 1,
or 2, or 3, or 7 intervening syllables.
If the separate syllables are designated by the positions which they held in the original arrangement, the following scheme
results:
I(1) I(2) I(3) . . . . . . . . . . . . . . . . . . . . . . . . I(15) I(16)
II(1) II(2) II(3) . . . . . . . . . . . .
. . . . . . . . . . II(15) II(16)
.
.
.
VI(1) VI(2) VI(3) . . . . . . . . . . . . . . . . . . . . VI(15) VI(16)
By using the same scheme the derived groups appear as follows:
By Skipping 1 Syllable
I(1) I(3) I(5) . . . . . . . I(15) I(2) I(4) I(6) . . . . . . . I(16)
II(1) II(3)
II(5) . . . . . II(15) II(2) II(4) II(6) . . . . . II(16)
.
.
.
VI(1) VI(3) . . . . . . . VI(15) VI(2) VI(4) .
. . . . . . VI(16)
By Skipping 2 Syllables
I(1) I(4) I(7) I(10) I(13) I(16) I(2) I(5) I(8) I(11) I(14) I(3) I(6) I(9) I(12)
I(15)
II(1) II(4) I(7) . . . . . . . .II(16) II(2) II(5) . . . . . . II(14) II(3) II(6) . . . . . . .II(15)
.
.
.
VI(1)
VI(4) . . . . . . . . . VI(16) VI(2) VI(5) . . . . . VI(14) VI(3) VI(6) . . . . . VI(15)
By skipping 3 syllables
I(1) I(5) I(9) I(13) I(2) I(6) I(10) I(14) I(3) I(7) I(11) I(15) I(4) I(8) I(12)
I(16)
II(1) II(5) . . . . . . II(2) II(6) . . . . . . . II(3) II(7) . . . . . . . . II(4) II(8). . . . .II(16)
.
.
.
VI(1)
VI(5) . . . . . VI(2) VII(6) . . . . . . VI(3) VI(7) . . . . . . . VI(4) II(8). . . . VI(16)
By Skipping 7 Syllables
I(1) I(9) II(1) II(9) III(1) III(9) IV(1) IV(9) V(1) V(9) VI(1) VI(9) I(2) I(10) II(2) II(10)
III(2) III(10)
IV(2) IV(10) V(2) V(10) VI(2) VI(10) I(3) I(11) II(3) II(11)III(3) III(11) IV(3) IV(11)
.
.
.
V(7) V(15) I(8)
I(16) II(8) II(16) III(8) III(16) IV(8) IV(16) V(8) V(16) VI(8) VI(16)
As a glance at this scheme will show, not all the neighboring syllables of the derived series were originally separated
by the number of syllables designated. In some places in order to again obtain series of 16 syllables1 greater jumps were
made; but in no case was the interval less. Such places are, for example, in the series in which two syllables are skipped,
the transitions from I(16) to I(2) and from I(14) to I(3). In the series in which 7 intermediates were jumped, there are seven
places where there was no previous connection between successive syllables since the syllables in question came from different
series and the different series, as has been often mentioned, were learned independently. The following is given in illustration:
I(9) II(1), II(9) III(1), etc. The number of these breaks varies with the different kinds of derivation, but in each case
is the same as the number of skipped syllables. On account of this difference, the derived series suffer from an inequality
inherent in the nature of the experiment.
In the course of the experiment the skipping of more than 7 syllables was shown to be desirable, but I refrained from carrying
that out. The investigations with the six 16-syllable series were carried quite far; and if series had been constructed using
greater intervals, the breaks above mentioned would have had too much dominance. The derived series then contained ever fewer
syllable-sequences for which an association was possible on the basis of the learning of the original arrangement; they were
ever thus more incomparable.
The investigations were carried on as follows: -- Each time the six series were learned in the original order and then
24 hours later in the derived and the times required were compared. On account of the limitation of the series to those described
above the results are, under certain circumstances, open to a serious objection. Let it be supposed that the result is that
the derived series are actually learned with a certain saving of time, then this saving is not necessarily due to the supposed
cause, an association between syllables not immediately adjacent. The argument might, rather, run as follows. The syllables
which are first learned in one order and after 24 hours in another are in both cases the same syllables. By means of the first
learning they are impressed not merely in their definite order but also purely as individual syllables; with repetition they
become to some extent familiar, at least more familiar than other syllables, which had not been learned just before. Moreover
the new series have in part the same initial and final members as the old. Therefore, if they are learned in somewhat less
time than the first series required, it is not to be wondered at. The basis of this does not necessarily lie in the artificial
and systematic change of the arrangement, but it possibly rests merely on the identity of the syllables. If these were repeated
on the second day in a new arrangement made entirely by chance they would probably show equally a saving in work.
In consideration of this objection and for the control of the remaining results I have introduced a further, the fifth,
kind of derived series. The initial and final syllables of the original series were left in their places. The remaining 84
syllables, intermediates, were shaken up together and then, after chance drawing, were employed in the construction of new
series between the original initial and final series. As a result of the learning of the original and derived series there
must in this can also be revealed how much of the saving in work is to be ascribed merely to the identity of the syllable
masses and to the identity of the initial and final members of the separate series.
Section 37. Results. Associations of Indirect Sequence
For each group of original and derived series 11 double tests were instituted, 55 therefore in all. These were distributed
irregularly over about 9 months. The results were as follows:

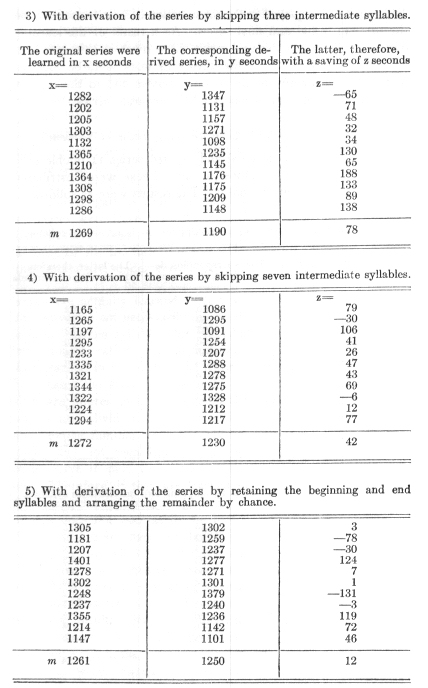
To summarize the results: The new series- formed by skipping 1, 2, 3 and 7 intermediate members were learned with
an average saving of 152, 94, 78 and 42 seconds. In the case of the construction of a new series through a mere permutation
of the syllables, there was an average saving of 12 seconds.
In order to determine the significance of these figures, it is necessary to compare them with the saving in work in my
case in the relearning of an unchanged series after 24 hours. This amounted to about one third of the time necessary
for the first learning in the case of 16-syllable series, therefore about 420 seconds.
This number measures the strength of the connection existing between each member and its immediate sequent, therefore the
maximal effect of association under the conditions established. If this is taken as unity, then the strength of the connection
of each member with the second following is a generous third and with the third following is a scant fourth.
The nature of the results obtained confirm -- for myself and the cases investigated -- the second conception given above
and explained by means of a quotation from Herbart. With repetition of the syllable series not only are the individual terms
associated with their immediate sequents but connections are also established between each term and several of those which
follow it beyond intervening members. To state it briefly, there seems to be an association not merely in direct but also
in indirect succession. The strength of these connections decreases with the number of the intervening numbers; with a small
number it was, as will be admitted, of surprising and unanticipated magnitude.
No evidence has been secured, however, establishing the facilitation of the process of relearning a series by means of
the identity of the syllables and the identity of the initial and final terms.
Section 38 Experiments with Exclusion of Knowledge
I have hitherto not stated the probable errors of the results, in order to discuss their reliability more fully at this
time.
When I started upon the experiment I had no decided opinion in favor of the final results. I did not find facilitation
of the learning of the derived series essentially more plausible than the opposite. As the numbers more and more bespoke the
existence of such facilitation, it dawned upon me that this was the correct and natural thing. After what has been said above
(p. 27ff [middle of chapter III]) one might think that in the case of the remaining experiments, this idea has
possibly favored a more attentive and therefore quicker learning of the derived series, and so has, at least, decidedly strengthened
the resulting saving in work, even if it has not caused it altogether.
For the three largest of the numbers found, -- consequently, for the facilitation of the work which took place in the case
of the omission of 1, 2, and 3 intervening syllables -- this objection is of slight significance. For these are proportionately
so large that it would be attributing too much to an involuntary heightening of a state of attention, voluntarily concentrated
without this to the utmost, if an actual influence is ascribed to it here. Moreover, the gradation of the numbers, decisively
issuing as they do from the distribution of the individual values and running parallel with the number of skipped intermediate
terms, is inconceivable on any such hypothesis as this. For the supposed greater concentration of the attention could clearly
work only in general. How could it possibly bring about so regular a gradation of numbers in the case of tests which were
separated from each other by weeks and months?
The objection presented above could render doubtful only the fourth result, the proportionally slight saving in the learning
of series formed from other series by skipping seven intermediate terms.
Clearly in this case the exact determination of the difference is of especial interest because of the significant size
of the interval over which an association took place.
In the case of the present investigations there exists the possibility of so arranging them that knowledge concerning the
outcome of the gradually accumulating results is excluded and so that consequently the disturbing influence of secret views
and desires disappears. I have accordingly instituted a further group of 30 double tests in the following way as a control
of the above results, and especially of the least certain of them.
On the front side of a page were written six syllable series selected by chance and on the reverse side of the same sheet
six series formed from them by one of the methods of derivation described above (p.97 [Section 36]). For each of the five
transformations 6 sheets were prepared. The fronts and backs of these could be easily distinguished but not the sheets themselves.
The thirty sheets were shuffled together and then laid aside until any memory as to the occurrence of the separate syllables
in definite transformations could be considered as effaced. Then the front side, and 24 hours later, the reverse side
of a given sheet were learned by heart. The times necessary for learning the separate series were noted, but they were not
assembled and further elaborated until all 30 sheets had been completed. Following are the numbers.

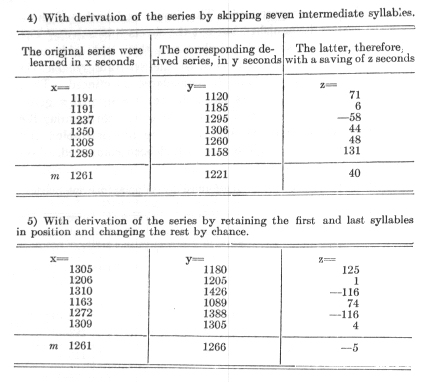
By derivation of the transformed series by skipping 1, 2,3, 7 intermediate syllables, the derived series were therefore
learned with an average saving of 110, 79, 64 40 seconds. On the contrary with derivation of the series by permutation of
the syllables the learning required an average increase in expenditure of 5 seconds.
Taken as a whole, these last results exactly confirm, as can be seen, the result that was obtained at the beginning. The
number of these experiments was proportionally small and, during the course of each experiment, there was complete exclusion
of knowledge as to results. In spite of these facts and although the numbers, considered individually, seem to be distributed
without regard to law, their grouping, when taken as a whole, is seen to be in conformity to a simple law. The fewer are the
intervening members which separate two syllables of a series which has been learned by heart, the less is the resistance offered
by these separated syllables to their being learned in a new order. And, in the same way, the fewer are these intervening
terms, the stronger are the bonds which, as a result of the learning of the original series, connect the two syllables across
the intervening members.
In addition to agreeing in their general course, the numbers for both groups of experiments also agree in the following
respect. The difference between the first and second numbers has the greatest value, and that between the second and third
has the least value. On the other hand, it is surprising that, with respect to their absolute size, the numbers of the second
group are throughout smaller than those of the first. Two causes may be brought forward in explanation of this behavior, which,
considering the conformity of the numbers, can scarcely be accidental. It may be that here is actually revealed that influence
of expectation which has already been mentioned. On the basis of this hypothesis, the explanation of the fact that the numbers
of the first group come out somewhat too large is that, in the course of the experiment, the existence of a saving in work
in the case of the derived series was anticipated, and for this reason the learning of the series took place involuntarily
with a somewhat greater concentration of attention. On the other hand, it may be that, in consequence of the excluded knowledge,
there has been at work in the case of the numbers of the second group a disturbing element which has made them smaller. Here,
to be sure, during the learning of the derived series a very lively curiosity developed concerning the category of transformation
to which the series which had just been learned belonged. That this must have had a distracting, and therefore retarding,
influence is probable not only in itself but also through the result obtained from the series derived by permutation of syllables.
It was to be expected that the identity of the syllables, as well as of the initial and end terms, would make itself felt
in this case by a saving of work, however small that saving might be. The latter effect appears, it is true, in the experiments
of the first group. With those of the second group, however, there is noticeable, instead of this saving of work, a slight
additional expenditure of time. This, if it is not merely accidental, can scarcely be explained otherwise than through the
distracting curiosity mentioned.
It is possible that both influences were at work simultaneously so that the first experiments gave results which were somewhat
too high; and the second, results that were somewhat too low. It is allowable, under this hypothesis, to put the two sets
of figures together so that the contrasting errors may compensate each other. In this way there was finally obtained out of
the 85 double tests the following table.
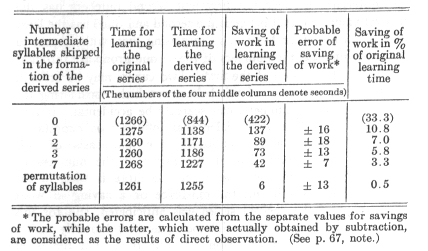
Section 39. Discussion of Results
In the foregoing table an especial interest, it seems to me, is connected with the last, and also with the next to the
last, row of numbers. When there was complete identity of all the syllables and the initial and end terms were left in their
places, the average saving of time for 17 tests dealing with the learning of the derived series was so slight that it was
hardly to be determined. It fell within half of its probable error. The syllables were, therefore, in themselves, outside
of their connection, so familiar to me that they did not become noticeably more familiar after being repeated 32 times. On
the contrary when a related series was repeated the same number of times, each syllable became so firmly bound to the syllable
which followed 8 places beyond that 24 hours later the influence of this connection could be determined in no doubtful fashion.
It attains a value 6 times the probable error. Its existence, therefore, must be considered to be fully proved although naturally
we cannot be so sure that its size is exactly what it was found to be in the experiments. Although its absolute value is small,
yet its influence amounts to one tenth of that of the connection which binds every member to its immediate successor. It is
so significant, and at the same time the decrease in the after-effect of connections which were formed over 2, 3, 7 intervening
members is so gradual a one, that the assertion can be made, am these grounds alone, that even the terms which stand still
further from one another may have been bound to each other subconsciously by threads of noticeable strength at the time of
the learning of the series.
I will summarise the results so far given in a theoretical generalisation. As a result of the repetition of the syllable-series
certain connections are established between each member and all those that follow it. These connections are revealed by the
fact that the syllable-pairs so bound together are recalled to mind more easily and with the overcoming of less friction than
similar pairs which have not been previously united. The strength of the connection, and therefore the amount of work which
is eventually saved, is a decreasing function of the time or of the number of the intervening members which separated the
syllables in question from one another in the original series. It is a maximum for immediately successive members. The precise
character of the function is unknown except that it decreases at first quickly and then gradually very slowly with the increasing
distance of the terms.
If the abstract but familiar conceptions of 'power,' 'disposition,' be substituted for the concrete ideas of saving in
work and easier reproduction, the matter can be stated as follows. As a result of the learning of a series each member lass
a tendency, a latent disposition, to draw after itself, at its own return to consciousness, all the members of the series
which followed it. These tendencies are of varying strength. They are the strongest for the members which immediately follow.
These tendencies are accordingly in general most easily demonstrable in consciousness. The series will return in its original
form without the intervention of other influences while the forces directed to the resuscitation of the remaining members
can be explicitly demonstrated only by the introduction of other conditions.
It is naturally not conceivable that by a mere caprice of nature the validity of the principles discovered should be limited
exclusively to the character of the material in which they were obtained -- i.e., to series of nonsense syllables.
They may be assumed to hold in an analogous way for every kind of idea-series and for the parts of any such series. It goes
without saying, wherever relations exist between the separate ideas, other than those of temporal sequence and separation
by intermediate members, these forces will control the associative flow, not exclusively, but with reference to all the modifications
and complications introduced by relations of various affinities, connection, meaning, and the like.
At any rate, it will not be denied that the doctrine of Association would gain through a general validity of these results
a genuine rounding out and, so to say, a greater reasonableness. The customary formulation, "ideas become associated if they
are experienced simultaneously or in immediate succession," has something irrational about it. If the immediacy of succession
is taken precisely, the principle contradicts the most common experiences. If it is not taken exactly, then it is hard to
state what kind of sequence is properly meant At the same time it is not clear why a sequence not quite direct should have
an advantage which suddenly disappears in the case of a sequence still more indirect. As we now know, the directness or indirect-ness
of the sequence is without effect upon the general nature of what happens between ideas which succeed each other. In both
cases connections are formed which on account of their complete similarity can be designated only by the common term, Association.
But these are of different strength. As the succession of united ideas approaches ideal immediacy the connecting threads grow
stronger, and in proportion as it departs from this ideal, these threads grow weaker. The associations between more distant
terms, although actually present and demonstrable under proper conditions have, nevertheless, on account of their slight strength,
practically no significance. The associations between adjacent terms are, on the contrary, of relatively great importance,
and will make their influence abundantly felt. Of course, if the series were left entirely to themselves and if they were
always produced in precisely the same order, for each term there would appear only one association, the relatively strongest
-- namely, that with the immediately succeeding term. But series of ideas are never left to themselves. The rich and quickly
changing order of events brings them into the most manifold relations. They return with their members in the most varied combinations.
And then, under certain circumstances, the stronger of these less strong associations between more distant terms must find
opportunity to authenticate their existence and to enter into the inner course of events in an effective way. It is easy to
see how they must favor a more rapid growth, a richer differentiation, and a many-sided ramification of the ideas which characterise
the controlled mental life. Of course they also favor a greater manifoldness, and so apparently a greater arbitrariness and
irregularity, in mental events.
Before I proceed further, I wish to add a few words concerning the above mentioned (p.91 [Section 35]) derivation of the
association of successive ideas from the unitary consciousness of a unitary soul. There is a certain danger in bringing together
a present result with one found previously. I mentioned above (p.47 [beginning of Chapter V]) that the number of syllables
which I can repeat without error after a single reading is about seven. One can, with a certain justification, look
upon this number as a measure of the ideas of this sort which I can grasp in a single unitary conscious act. As we just now
saw, associations are formed of noticeable strength over more than seven intervening members, therefore between the beginning
and end of a nine-syllable series. And on account of the size of the numbers obtained and the nature of their gradation, it
seems probable that, even with a larger number of syllables, connections would be formed between their extremes. If, however,
associations are built between members too far separated to be held together in a single conscious act, it is no longer possible
to explain the presence of those associations on the basis of the simultaneous presence of the united ideas in consciousness.
However, I recognise that those for whom such a derivation is a cherished matter are not necessarily forced by the above
discussion to abandon their conception. Such are those who consider the unitary acts of a unitary soul as something more original,
intelligible, transparent or better worthy of belief than the simple facts of association described above, so that the reduction
of the latter to the former would be a noteworthy achievement. One needs but to say that, in the case of an unfamiliar sequence
of syllables, only about seven can be grasped in one act, but that with frequent repetition and gradually increasing familiarity
with the series this capacity of consciousness may be increased. So, for example, a series of 16 syllables, which have been
thoroughly memorised, may be present in a single conscious act. Accordingly this "explanation" is freely available. Those
for whom it was of value in the case of association by simultaneity or immediate succession can employ it fully as well for
our case of indirect sequence. And because of the modest requirements which in psychology are so often imposed upon explanations,
this view will doubtless for a long time serve to make dim the vision and so prevent the frank recognition of this as one
of the most wonderful of all riddles, and it will also act as a hindrance in the search for its true understanding.
Section 40. Reverse Associations
Of the many problems which spring out of the results presented I have been able for the time being to investigate only
a few and these by means of only a small number of experiments.
As a result of the frequent repetition of a series -- a, b, c, d . . . -- certain connections -- ab, ac,
ad, bd, etc. -- are formed. The idea a, whenever and however it returns to consciousness, has certain tendencies
of different strength to bring also with it to consciousness the ideas b, c, d. Are now these connections and tendencies
reciprocal? That is, if at any time c and not a is the idea by some chance revived, does this have, in addition
to the tendency to bring d and e back with it, a similar tendency in the reverse direction towards b and
a? In other words: -- As a result of the previous learning of a, b, c.[sic] d, the sequences
a, b, c, a, c, e, are more easily learned than any grouping of equal length of syllables previously unknown
such as p, q, r. . . . Is the same thing true of the sequences c b a, and e c a? As a result
of manifold repetition of a series are associations also formed in the reverse order?
The views of the psychologists seem to be divergent upon this point. One side call attention to the undoubted fact that
in spite of complete mastery of, say, the Greek alphabet a person is not at all in a position to repeat it readily backwards
if he has not specially studied and practiced it in this form.
The other side make extensive use of reverse associations, as of something quite intelligible, in their explanation of
the origin of voluntary and purposive movements. According to them the movements of the child are at first involuntary and
accidental. With certain combinations of these, intensely pleasurable feelings result. In the case of movements as of feelings,
memory traces remain which, by repetition of the occurrences, are always more closely associated with each other. If this
connection has attained a certain strength, the mere idea of the agreeable feeling leads backwards to the idea of the movement
which aroused it; then comes the actual movement and with it also the actual sensed feeling.
The conception of Herbart, which we learned to know above (p. 94 [Section 35]), holds the middle course between these two
views. The idea c, which appears in the course of a series, fuses with the ideas b and a, which have
preceded it and which are yet present although becoming dim. If c is later on reproduced, it brings b and a
with it but dimmed, not fully uninhibited or clearly conscious. With the sudden arousal of a member out of the midst of a
series we survey that which preceded "at once in graded clearness"; but never does it happen that the series runs off in reverse
order. To the member which springs up in consciousness there succeed in due order and in complete consciousness those terms
which followed it in the original series.
For the purpose of testing the actual relations I carried out an experiment entirely similar to the previously described
investigations. Out of groups each composed of six 16-syllable series arranged by chance new groups were derived either through
mere reversal of the sequence or by that plus the skipping of an intermediate syllable. Then the two sets of groups were learned
by heart, the derived form 24 hours later than the original.
If the scheme for the original form is written as follows:
I(1) I(2) 1(3) . . . . . . . I(15) I(16), then the corresponding derived series is thus designated:
In the case of mere reversal of the syllable sequence;
I(16) I(15) I(14) . . . . . . . . I(2) I(1),[sic]
In the case of reversal plus skipping of an intermediate syllable,
I(16) I(14) I(12). . . . . . . I(4) I(2) I(15) I1(13). . . . . . . I(3)I(1).
For the first kind of derivation I have carried out ten experiments; for the second, only four.
The results are as follows:

In relation to the time of learning the original series the saving amounts to 124 per cent.

In relation to the time of learning the original series the saving amounted to ~ per cent.
As a result of the learning of a series certain connections of the members are therefore actually formed in a reverse as
well as in a forward direction. These connections are revealed in this way, that series which are formed out of members thus
connected are more easily learned than similar series, whose individual members are just as familiar but which have not been
previously connected. The strength of the predispositions thus created was again a decreasing function of the distance of
the members from each other in the original series. It was, however, considerably less for the reverse connections than for
the forward ones, the distances being equal. With an approximately equal number of repetitions of the series the member immediately
preceding a given member was not much more closely associated with it than the second one following it; the second preceding
-- so far as may be determined on the basis of these few researches -- scarcely as firmly as the third following.
If one could assume a more general validity for this relation found here first in connection with syllable series, the
mutually opposed experiences just mentioned would, I believe, become thoroughly intelligible. Where a series consists of only
two members -- as in the case of the connection between a simple idea of movement and that of an agreeable feeling -- then,
by means of frequent repetition the end term will acquire so strong a tendency to call up after itself the initial term that
the latter will actually appear. For the bringing up of the term first preceding it is the only thing for which, as a result
of the many repetitions, the second term has acquired a predisposition. But, no matter how many repetitions there may be in
the case of a long series, it will never happen on the arousal of a middle term that the series will reappear in a reverse
order. For, however easily the immediately preceding term may connect itself with the one for the moment aroused, the immediately
succeeding term will appear more easily by far, and so will win the victory, provided other influences do not intervene.
No matter how thoroughly a person may have learned the Greek alphabet, he will never be in a condition to repeat it backwards
without further training. But if he chances to set out purposely to learn it backwards, he will probably accomplish this in
noticeably shorter time than was the case in the previous learning in the customary order. The objection is not in point that
a poem or speech which has been committed to heart is not necessarily learned more quickly backwards than it was originally
forwards. For with the learning in reverse direction the numerous threads of inner connection on which rapid learning of meaningful
material in general depends will be brought to nothing.
Section 41. The Dependence of Associations of Indirect Sequence upon the Number of Repetitions
The connection set up as a result of many repetitions between the immediately succeeding members of an idea- or syllable-series
is a function of the number of repetitions. As a result of the investigations of Chapter VI, which were purposely directed
to the discovery of this relation, an approximate proportionality, within tolerably wide limits, has been made out between
the number of repetitions and the strength of the connections established by them. The latter was measured, precisely as in
the investigations of the present chapter, by the amount of work saved in relearning the connected series after 24 hours.
If now, as a result of repetitions, connections are also set up between members of a series which are not immediately successive,
the strength of the latter is naturally also in some way dependent upon the number of repetitions. The question arises in
what form the different dependence occurs in this case. Does a proportionality exist here also? If the number of repetitions
is made greater, will the threads of separate strength, which bind together all the members of a series learned by heart,
increase in strength in the same proportion? Or is the nature and rate of their increase in strength a different one as is
the case with the strength of the threads themselves? On the basis of our present knowledge neither the one nor the other
of these possibilities can be declared self-evident
To facilitate an insight into the actual conditions I have instituted a few preliminary experiments in the following way.
Six aeries of 16 syllables each were impressed upon the memory by a 16- or 64-fold attentive repetition. After 24 hours an
equal number of derived series of the same length, which had been obtained from those already learned
by skipping one intermediate syllable, were learned by heart to the first repetition. In order
to make the investigations useful in other ways, the series were derived in this case by a method somewhat different from
that described above (p. 97 [Section 36]). The latter method differs from the former in that here the odd-numbered syllables
of the original series were not followed by the even-numbered syllables of the same series. But all the odd-numbered syllables
of two original series were united to form a new 16-syllable series. Then the even-numbered syllables of the same original
series were united to form a second new series. The scheme of the derived series was therefore not, as above,
I(1) I(3) I(5) . . . . . . . . . . I(15) I(2) I(4) . . . . . I(16)
II(1) II(3) II(5) . . . . . . . . II(15)
II(2) II(4) .. . . . II(16)
but rather
I(1) I(3) I(5) . . . . . . . . . . I(15) II(1) I(3) . . . . . I(15)
I(2) I(4) I(6) . . . . . . . . . I(16)
II(2) II(4) . . . . . II(16)
The effect of the derivation upon the learning of the derived series, cannot, as it seems, be essentially affected through
this slight change. Here, as in the above described method of derivation, the syllables which during the first learning had
been separated from each other by an intervening syllable were learned 24 hours later in immediate succession.
For each number of repetitions used in learning I made 8 double tests, which gave the following results:
Number of repetitions employed for the impression of each of the original series:
Number of seconds required for learning the six derived series after 24 hours (including the recital):
| |
1178 |
1157 |
| |
1216 |
982 |
| |
1216 |
1198 |
| |
950 |
1148 |
| |
1358 |
995 |
| |
1019 |
1017 |
| |
1191 |
1183 |
| |
1230 |
1198 |
| |
--------------- |
|
|
Average |
1170 |
1109 |
|
Probable error |
30 |
22 |
On account of the small number of experiments the resulting averages are, unfortunately, not very exact; but the general
character of the results would remain the same even if we considered the value false within the whole range of the probable
error. This character becomes apparent upon comparison with the values given above (p.56 [middle of Chapter 6]) for learning
by heart six 16-syllable series which had not previously been learned. This took place in 1,270 seconds. After the original
series had been repeated 16 times, the derived series was learned with a saving of about 100 seconds; after repetition 64
times, with a like saving of 161 seconds. Quadrupling the repetitions resulted in increasing the saving only a little more
than half as much again. The increase in strength of the associations reaching over an intermediate member was in nowise proportional
to the number of repetitions, for the cases studied, not even within the limits for which this was noticeably the case for
associations from one member to its immediate successor. On the contrary the effect of the repetitions in the case of associations
of indirect sequence decreased considerably sooner and more quickly than in the case of those of direct sequence.
There is very close agreement between the pair of values just found and the number given above (p.99, I [Section 37]) --
the procedure being, as here, without the exclusion of knowledge -- for the learning of derived series which the day before
had been learned in their original form to the point of first possible reproduction. This number, it is true, was obtained
under somewhat different conditions. In the first place, not always were the same number of repetitions employed for learning,
but each time as many as were required for the first possible reproduction -- i.e., not exactly, but on the average,
32. Moreover, the nature of the derivation of the senses was somewhat different, as was stated above. But these differences
have little weight in the case of numbers which otherwise could have little claim to exactness. I adduce therefore this value
for comparison, and in addition the numbers give in Chapter VI for the influence of repetitions on the relearning of the same
untransformed series. Here then is the table.

I call attention again to the fact that the numbers given above are in part rather inexact and that they were gained under
very limited conditions. However, it is allowable to sketch summarily and with hypothetical elaboration the view which these
results make appear to be the most probable explanation of an important group of inner processes and which fills pleasingly
and completely a hitherto empty place in our knowledge.
With the imprinting and internal fixation of an idea-series through its manifold repetition, inner connections, associations,
are woven between all the separate members of the series. The nature of these is such that series made out of members thus
associated are picked up and reproduced more easily, with less resistance to be overcome, than similar series made up of members
not previously associated. Their nature can also be stated in this way, that each member of the series has the definite tendency
on its own return to consciousness to bring back others with it. These connections, or tendencies, are of different strength
from several different points of view. For the more distant members of the original series they are weaker than for the nearer;
for specific distances backwards they are weaker than for the same distances forward. The strength of all the connections
increases as the number of repetitions increases. But the originally stronger threads between the nearer members are strengthened
considerably more quickly than the weaker ones which connect the more distant terms. The more, therefore, the number of repetitions
increases, the stronger, both absolutely and relatively, become the connections between immediately successive terms. To the
same degree the more exclusive and dominant becomes the tendency of each term at its own return into consciousness to draw
after itself that term which had always immediately followed it during the repetitions.
Section 42. Indirect Strengthening of Associations
I conclude with the mention of a noteworthy fact which appeared incidentally in connection with the investigations mentioned
in the preceding paragraphs. On account of the uncertainty of the numerical results which come into consideration, I can call
attention to it only with great reserve. I cannot, how-ever, pass it by altogether because it is probable in itself, and because,
with further confirmation, it will throw a characteristic light on inner processes which are actually present but which remain
unconscious. It will also reveal the relative independence of these processes from conscious accompaniments, as I have shown
above (§ 24).
The derivation of the transformed series in the case of the last mentioned investigations was accomplished, as has been
stated, in the following way. Out of two 16-syllable series selected by chance, first all the odd-numbered syllables were
combined to form a new series and then all the even-numbered to form a second series which followed in immediate succession.
In the case of a group consisting of six series of this sort, therefore, the derived series II contained nothing but syllables
which in the first process of memorising had followed immediately upon the corresponding members of series I. The derived
series IV bore a similar relation to series III, and series VI to series V. The following phenomenon appeared, which is the
peculiar relation to which I wish to call attention. Less time was required for learning by heart series II, IV, VI on the
average than for series I, III, V, although in all the other groups of series, whether original or derived, the converse was
the case.
I adduce some numerical data in evidence of this relation.
From all the experiments with six series of 16 syllables which were learned to the point of the first recital, ten immediately
successive experiments are chosen by chance for two different time-periods. The times for committing to memory series I, III,
V are combined in calculation, as are also those for series II, IV, VI.
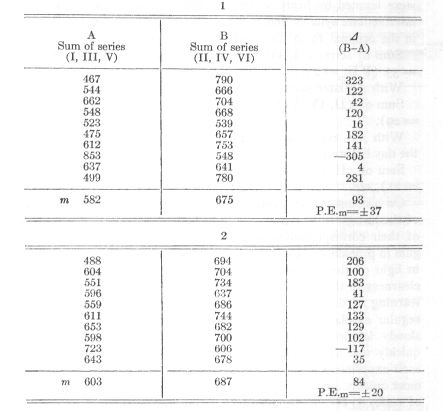
The sum of series II, IV and VI, found by averaging the ten experiments, is here in both cases, as can readily be seen,
considerably greater than the sum of series I, III, V. The differences are, to be sure, of very different amounts for the
separate experiments, and in one case they have a pronounced negative value; but these fluctuations are represented in the
large probable error of the differences of the averages; and, in spite of the size of these errors, the positive character
of the differences may be considered as fairly certain.
In all other investigated cases the following result appears: there are large fluctuations of the differences in the individual
experiments, but a combination of the several experiments shows a decisive predominance for series II, IV, VI although the
surplus is smaller than in the case of the two experiments in question. Thus in the case of it earlier tests in which series
were learned by heart which had been derived by skipping one intermediate syllable and which had been learned the day before
in the original form the results were (p.99, I [Section 37]):
Sum of series (II, IV, VI) minus Sum of series (I, III, V) = 33 (P.E.m = 23)~
With six later tests of the same sort (p.103, I [Section 37]):
Sum of (II, IV, VI) minus Sum of (I,III, V) = 42 (P.E.m = 29).
With ten experiments with series which had been repeated the day before 16 times each (p. 55 [beginning of Chapter 6]):
Sum of (II, IV, VI) minus Sum of (I, III, V) = 17 (P.E.m = 21), etc.
On account of the largeness of the probable error a single one of the last given figures would have little significance.
By means of their correspondence as to the nature of the difference they gain in probability, and the phenomenon becomes quite
intelligible in light of the results of Section 18. There, and with especial dearness in the case of 16-syllable series, it
was shown that the learning of the individual series occurred in the form of fairly regular oscillations. These were of such
a sort that a relatively slowly learned series followed one learned relatively more quickly and vice versa (p.43 [end of Chapter
4], Fig. 3). Since in the case of each experiment the first series was learned on the average the most quickly and the second
the most slowly, by the combination of series I,III, V the average minima are united and of series II, IV, VI the average
maxima. The difference, S (II, IV, VI) minus (I,III, V) is, therefore, in general positive.
Accordingly it must be surprising that in the case of both the groups of tests mentioned in the preceding paragraphs, this
difference is on the contrary of a negative sign.

The fluctuations of the numbers for the separate experiments are also in this case very great. However, it is evident on
the first glance and without further comparison that a strong displacement of the differences to the negative side has taken
place. This fact is also expressed by the averages. In contrast with previous results, the series II, IV, VI were learned
in somewhat shorter time than series I, III, V.
That this exception rests on mere chance is possible but not very probable. The probable errors, although large, are not
large enough to indicate this.
I would sooner fear that it was a case of disturbance of the results through the oft-mentioned source of error, anticipation
of the outcome (p.27 ff. [Chapter III] and p. 101[Section 37]). During the progress of the experiment I believed with increasing
certainty that I could foresee the smaller expenditure of time for the learning of series II, IV, VI, and it was only because
I thought something of this sort that I changed the method of derivation of the transformed series. I cannot, therefore, exclude
the possibility that, merely on the basis of this hidden presupposition and in a manner altogether unrevealed to consciousness,
a greater concentration of attention was present in learning series II, IV, VI than in learning series I, III, V. However,
this assumption is not to be taken positively as the correct one. The assumption that the whole of the difference found is
to be traced back to the influence of this source of error would involve the ascription of a pretty large function to an involuntary
and completely unconscious accommodation of attention due to a secret expectation.
There remains, accordingly, a certain probability for the third possibility, namely, that the contrasting character of
the average differences has in part at least an objective basis, that the more rapid learning of the derived series, II, IV,
VI, was in part due to their manner of derivation.
The proper way in which to think of this causation would become dear only by the introduction of physiological conceptions
which must first be constructed or at least remodelled. If use is made of the language of psychology, then, as in the case
of all unconscious processes, expression can be only figurative and inexact.
As a result of the learning by heart of a series in the original form the separate syllables, we must say, retain fairly
strong tendencies upon their own return to consciousness to bring after them the syllables which immediately succeeded them.
If, therefore, the syllables 1, 3, 5, etc., return to consciousness, the syllables 2, 4, 6, etc., have a tendency also to
appear. This tendency is not strong enough to bring about as a consciously perceivable event the actual appearance of 2, 4,
6. The latter are in evidence only in a certain inner condition of excitability; something takes place in them which would
not have occurred if 1, 3, 5 had not been repeated. They behave like a forgotten name which one attempts to recollect.
This is not consciously present; on the contrary, it is being sought. In a certain way, however, it is undeniably present.
It is on the way to consciousness, as one might say. For if ideas of all sorts were called up which stood in connection with
the earlier experienced name, a person could usually tell whether they agreed with the one now sought for but not yet found,
or not. As a result of the frequent repetition of the syllables 1, 3, 5 previously connected with the syllables 2, 4, 6, the
latter were placed in a similar slightly pronounced condition of excitation, lying between conscious appearance on the one
side and simple non-appearance on the other. And this excitation has, as it now appears from our tests, a result altogether
similar to that of actual return to consciousness. Inner connections are established between successively and internally aroused
syllables just as between syllables successively raised to consciousness, except that the former are naturally of less strength.
Secret threads are spun which bind together the series 2, 4, 6, not yet aroused to consciousness, and prepare the way for
its conscious appearance. Such threads existed already in greater strength as a result of the learning of the original series;
the present effect is that of strengthening somewhat connections already made. And that is nothing else than what was found
above: if two syllable-combinations -- 1, 3, 5 . . . and 2, 4, 6 . . . -- are frequently associated in consciousness (the
learning of the original series) then the subsequent learning of the second combination (derived series II, IV, VI) soon after
the learning of the first (derived series I, III, V) has considerably less resistance to overcome than the latter. A certain
strengthening of associations takes place, not only directly, through conscious repetition of the associated members,
but also indirectly through the conscious repetition of other members with which the first had been frequently connected.
This way of viewing the matter is a consequence of the assumption (which became necessary above, p. 109 [Section 39]) of
the formation of associative connections over more intervening members than could be comprehended in one clearly conscious
act. These connections would be very fruitful in the explanation of many surprising phenomena of memory and recollection,
but on account of the uncertainty of their experiential basis I refrain for the present from pursuing them further.
Footnotes
[1] Herbart, Lehrb. z. Psychol., Sect. 29. A similar "pleasing" view, as he calls it, was developed by Lotze, Metaphysik (1879)
p.527, with the modification that he attempts to eliminate the notion of varying strength of the ideas, which view he rejects.
In accordance with the view mentioned first above, he sees the real reason for a faithful reproduction of a series of ideas
in the fact that association is made only from one link to the following link. Accordingly, he teaches, in his Lectures on
Psychology (p. 22), "Any two ideas, regardless of content, are associated when they are produced either simultaneously
or in immediate succession -- i.e., without an intervening link. And upon this can be based without further artifice
the special ease with which we reproduce a series of ideas in their proper order but not out of that order. By "further artifice"
he seems to mean Herbart's attempt at an arrangement
[2] I have omitted to present a few tests with series of 16 syllables each from which this number was obtained,
because the results of the sixth chapter sufficiently cover this point. There (p. 55 [beginning of Chapter VI]), we saw that
six series of 16 syllables each, each series being repeated 32 times, could be memorised after 24 hours in an average of 863
seconds. 32 repetitions are, on an average, just necessary to bring about the first possible reproduction of series of 16
syllables each. Considering the close proportion which exists between the number of repetitions on a given day and the saving
of work on the next, it cannot much matter whether the series were repeated, each 32 times, or were memorised each to the
first possible reproduction. Since the latter requires about 1,270 seconds, the work of repetition on the following day amounts,
as stated above, to about two thirds of this time. The relative saving when 16-syllable series are relearned after 24 hours,
is, therefore, scarcely different from that found for series of 12 and 13 syllables (chapters VII and VIII), while
it gradually increases for still greater length of series.
|

